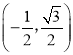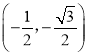题目内容
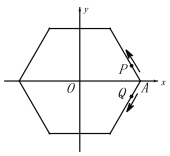
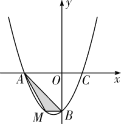
【题目】(2010河南23题)在平面直角坐标系中,已知抛物线经过![]() ,
,![]() ,
,![]() 三点.
三点.
(1)求抛物线的解析式;
(2)若点M为第三象限内抛物线上一动点,点M的横坐标为m,![]() 的面积为S.求S关于m的函数关系式,并求出S的最大值;
的面积为S.求S关于m的函数关系式,并求出S的最大值;
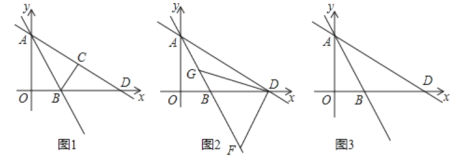
(3)若点P是抛物线上的动点,点Q是直线![]() 上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
上的动点,判断有几个位置能使以点P、Q、B、O为顶点的四边形为平行四边形,直接写出相应的点Q的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ,最大值为4;(3)符合条件的点
,最大值为4;(3)符合条件的点![]() 的坐标分别为
的坐标分别为![]()
【解析】
解:(1)设抛物线的解析式为![]() ,则有
,则有
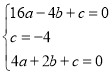 ,解得
,解得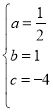 ,
,
∴抛物线的解析式为![]() ;
;
(2)如解图①,过点![]() 作
作![]() 轴于点
轴于点![]() .设
.设![]() 点的坐标为
点的坐标为![]() ,
,

则![]() ,
,![]() ,
,![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
![]() ;
;
(3)满足题意的![]() 点的坐标有四个,分别是(
点的坐标有四个,分别是(![]() ,4),(4,
,4),(4,![]() ),
),![]() 或
或![]() .
.
[解法提示]分情况讨论:①当![]() 为平行四边形的边长时,则
为平行四边形的边长时,则![]() ,如解图②:
,如解图②:
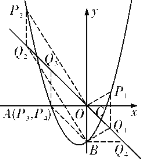
设![]() ,
,
当![]() 在
在![]() 上方时,
上方时,![]() ,
,
即![]() ,
,
解得![]() ,
,
![]() ;
;
当![]() 在
在![]() 下方时,
下方时,![]() ,
,
即![]() ,解得
,解得![]() (舍去),
(舍去),![]() ,
,
![]() ;
;
②当![]() 为平行四边形的对角线时,由图形的中心对称易得
为平行四边形的对角线时,由图形的中心对称易得![]() .
.
综上,符合条件的点![]() 的坐标分别为
的坐标分别为![]()

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案
相关题目
【题目】某校为了解全校学生假期主题阅读的情况(要求每名学生的文章阅读篇数,最少3篇,最多7篇),随机抽查了部分学生在某一周主题阅读文章的篇数,并制成下列统计图表.
某校抽查的学生文章阅读的篇数统计表
文章阅读的篇数(篇) | 3 | 4 | 5 | 6 | 7 |
人数(人) | 20 | 28 |
| 16 | 12 |

请根据统计图表中的信息,解答下列问题:
(1)求被抽查的学生人数和![]() 的值;
的值;
(2)求本次抽查的学生文章阅读篇数的中位数和众数;
(3)若该校共有800名学生,根据抽查结果,估计该校学生读书总数.
【题目】二次函数![]() 为常数,
为常数,![]() 中的
中的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
x | -1 | 0 | 3 |
y | n | -3 | -3 |
当![]() 时,下列结论中一定正确的是________(填序号即可)
时,下列结论中一定正确的是________(填序号即可)
①![]() ;②当
;②当![]() 时,
时,![]() 的值随
的值随![]() 值的增大而增大;③
值的增大而增大;③![]() ;④当
;④当![]() 时,关于
时,关于![]() 的一元二次方程
的一元二次方程![]() 的解是
的解是![]() ,
,![]() .
.