Question

6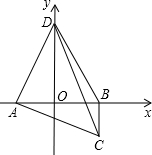．如图，在平面直角坐标系中，已知点A（m，0），点B（4，0）、C（4，m），其中m＜0，点D是y轴正半轴上的一点，且OD=AB，分别连接AD、AC、DB和DC．
（1）请直接写出D点的坐标（用含m的整式表示）；
（2）判断△DAC的形状并说明理由；
（3）是否存在实数m的值，使得S_{四边形DACB}=（6-3m）S_△DBC？若存在，请求出m的值；不存在，请说明理由．

Answer 1

分析 （1）先求出AB=4-m，则OD=4-m，即可解答；
（2）分别求出AD，AC，CD，根据勾股定理的逆定理进行判定，即可解答．
（3）存在，过点C作CF⊥y轴与点F，则点F的坐标为（0，m），根据OE∥CF，所以$\frac{OE}{CF}=\frac{OD}{DF}$=$\frac{4-m}{4-m-m}=\frac{4-m}{4-2m}$，求出OE=$\frac{4（4-m）}{4-2m}$，根据S_{四边形DACB}=（6-3m）S_△DBC即可解答．

解答 解：（1）∵点A（m，0），点B（4，0），
∴AB=4-m，
∵OD=AB，
∴OD=4-m，
∴D点的坐标为（0，4-m）．
（2）AD²=m²+（m-4）²=2m²-8m+16，AC²=（m-4）²+m²=2m²-8m+16，
CD²=4²+（m-4+m）²=4m²-16m+32，
∴AD=AC，AD²+AC²=CD²，
∴△DAC为等腰直角三角形．
（3）存在m的值，
如图，过点C作CF⊥y轴与点F，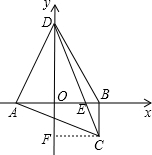

则点F的坐标为（0，m），
∵OE∥CF，
∴$\frac{OE}{CF}=\frac{OD}{DF}$=$\frac{4-m}{4-m-m}=\frac{4-m}{4-2m}$，
∴OE=$\frac{4（4-m）}{4-2m}$，
∵$\frac{{S}_{四边形ADBC}}{{S}_{△DBC}}=\frac{AB}{EB}=\frac{4-m}{EB}=\frac{4-m}{4-OE}$=$\frac{（4-m）（4-2m）}{4-4（4-m）}$=6-3m，
解得：m=2或-0.8．

点评 本题考查了坐标与图形的性质，解决本题的关键是根据图形求出相关点的坐标．