Question

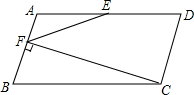如图，在平行四边形ABCD中，BC=2AB，E为AD中点，CF⊥AB于点F，连接EF．若∠B=70°，则∠FED=

 

度．

Answer 1

考点：平行四边形的性质,全等三角形的判定与性质

专题：

分析：延长FE，交CD延长线于M，连接CE，首先证明△AEF≌△DEM可得EM=EF，∠AFE=∠M，再根据直角三角形斜边上的中线等于斜边的一半可得∠M=∠1，然后根据∠B=70°可算出∠M=55°，进而可得∠FED的度数．

解答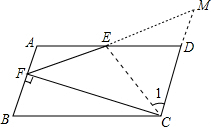：解：延长FE，交CD延长线于M，连接CE，
∵四边形ABCD是平行四边形，
∴AB∥CD
∴∠A=∠MDE，
∵E为AD中点，
∴AE=ED，
在△AEF和△DEM中，

∠A=∠EDM AE=ED ∠AEF=∠DEM

，
∴△AEF≌△DEM（ASA），
∴EM=EF，∠AFE=∠M，
∵CF⊥AB，
∴∠AFC=90°，
∴∠AFC=∠FCD=90°，
∵EM=EF，
∴EC=EM，
∴∠M=∠1，
∵四边形ABCD是平行四边形，
∴∠D=∠B=70°，∠A=110°，
∵ED=CD，
∴∠1=（180°-70°）÷2=55°，
∴∠M=55°，
∴∠AFE=55°，
∴∠AEF=180°-110°-55°=15°，
∴∠FED=165°．
故答案为：165．

点评：此题主要考查了平行四边形的性质，以及直角三角形的性质和全等三角形的判定和性质，关键是正确作出辅助线，证明∠AFE=∠M=∠1．