题目内容
6. 如图,一次函数y1=kx+b与y2=x+a的图象交点的横坐标为3,则下列结论:①k<0;②a>0;③当x<3时,y1>y2中,正确结论的个数是( )
如图,一次函数y1=kx+b与y2=x+a的图象交点的横坐标为3,则下列结论:①k<0;②a>0;③当x<3时,y1>y2中,正确结论的个数是( )| A. | 0 | B. | 3 | C. | 2 | D. | 1 |
分析 ①由一次函数y1=kx+b的图象过第一、二、四象限,即可得出k<0,由此即可得出①正确;②由一次函数y2=x+a的图象过第一、三、四象限,即可得出a<0,由此得出②错误;③根据两一次函数图象的上下位置关系即可得出当x<3时,y1>y2,即③正确.综上即可得出结论.
解答 解:①∵一次函数y1=kx+b的图象过第一、二、四象限,
∴k<0,①正确;
②∵一次函数y2=x+a的图象过第一、三、四象限,
∴a<0,②错误;
③观察函数图象,发现:
当x<3时,一次函数y1=kx+b的图象在一次函数y2=x+a的图象的上方,
∴当x<3时,y1>y2,③正确.
综上可知:正确的结论为①③.
故选C.
点评 本题考查了一次函数与一元一次不等式,解题的关键是逐条分析三个选项是否正确.本题属于基础题,难度不大,解决该题型题目时,熟悉一次函数图象与一次函数系数的关系是关键.

练习册系列答案
相关题目
17. 如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,则图中的全等三角形对数共有( )
如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,则图中的全等三角形对数共有( )
 如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,则图中的全等三角形对数共有( )
如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,则图中的全等三角形对数共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
14.陈文住在学校的正东200米处,从陈文家出发向北走150米就到了李明家,若选取李明家为原点,分布以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,则学校的坐标是( )
| A. | (150,200) | B. | (200,150) | C. | (-150,-200) | D. | (-200,-150) |
1.在直角三角形中,两条直角边的长分别为12和5,则斜边上的中线长是( )
| A. | 6.5 | B. | 8.5 | C. | 13 | D. | $\frac{60}{13}$ |
11.已知点(-1,y1),B(1,y2)都在直线y=-4x+3上,则y1,y2大小关系是( )
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
18.南涧无量樱花谷的樱花在12月中旬左右盛开,花朵绚丽迷人,吸引了众多海内外游客,去年到樱花谷参观的游客约为150000人,将这个数据用科学记数法表示为( )
| A. | 1.5×103 | B. | 1.5×104 | C. | 0.15×105 | D. | 1.5×105 |
15.在平面直角坐标系中,直线y=2x-6不经过( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.已知一次函数y=kx+b经过两点(x1,y1),(x2,y2),若k<0,则当x1<x2时,( )
| A. | y1<y2 | B. | y1>y2 | C. | y1=y2 | D. | 无法比较 |
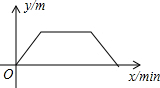 如图是王大爷早晨出门散步时,离家的距离y(m)与时间x(min)之间的变化关系,若用黑点表示王大爷家的位置,则王大爷散步行走的线路可能是( )
如图是王大爷早晨出门散步时,离家的距离y(m)与时间x(min)之间的变化关系,若用黑点表示王大爷家的位置,则王大爷散步行走的线路可能是( )