题目内容
已知四边形ABCD是正方形.
(1)若点E在正方形ABCD的内部,且△CBE是等边三角形,求∠AEB的度数;
(2)若点E在正方形ABCD的外部,且△CBE是等边三角形,求∠AEB的度数.
(1)若点E在正方形ABCD的内部,且△CBE是等边三角形,求∠AEB的度数;
(2)若点E在正方形ABCD的外部,且△CBE是等边三角形,求∠AEB的度数.
考点:正方形的性质,等边三角形的性质
专题:
分析:(1)根据正方形的性质得出AB=BC,∠ABC=90°,再由等边三角形的性质得出BE=BC,∠EBC=60°,得出AB=BE,∠ABE=30°,即可求出∠AEB;
(2)同(1)方法.
(2)同(1)方法.
解答:
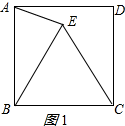 解:(1)如图1所示:∵四边形ABCD是正方形,
解:(1)如图1所示:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵△CBE是等边三角形,
∴BE=BC,∠EBC=60°,
∴AB=BE,∠ABE=90°-60°=30°,
∴∠AEB=
(180°-30°)=75°;
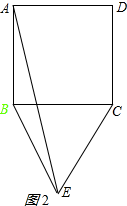 (2)如图2所示:
(2)如图2所示:
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵△CBE是等边三角形,
∴BE=BC,∠EBC=60°,
∴AB=BE,∠ABE=90°+60°=150°,
∴∠AEB=
(180°-150°)=15°.
 解:(1)如图1所示:∵四边形ABCD是正方形,
解:(1)如图1所示:∵四边形ABCD是正方形,∴AB=BC,∠ABC=90°,
∵△CBE是等边三角形,
∴BE=BC,∠EBC=60°,
∴AB=BE,∠ABE=90°-60°=30°,
∴∠AEB=
| 1 |
| 2 |
 (2)如图2所示:
(2)如图2所示:∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∵△CBE是等边三角形,
∴BE=BC,∠EBC=60°,
∴AB=BE,∠ABE=90°+60°=150°,
∴∠AEB=
| 1 |
| 2 |
点评:本题考查了正方形的性质和等边三角形的性质以及等腰三角形的判定与性质;根据正方形和等边三角形的性质得出等腰三角形是解题的关键.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
下列命题中,真命题是( )
| A、相等的角是对顶角 |
| B、两边及一角分别相等的两个三角形全等 |
| C、直角三角形的任意两角互余 |
| D、两角及其夹边分别相等的两个三角形全等 |
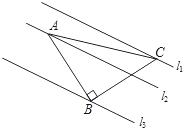 如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为3,则AC的长是( )
如图,已知△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为1,l2,l3之间的距离为3,则AC的长是( )A、
| ||
B、
| ||
C、
| ||
| D、5 |
下列计算正确的是( )
| A、a2+a3=a5 |
| B、a•a2=a2 |
| C、(ab)3=ab3 |
| D、(-a2)2=a4 |
下列说法正确的是( )
| A、有理数是有限小数 |
| B、无限小数是无理数 |
| C、数轴上的点与实数一一对应 |
| D、实数分为正实数和负实数 |
图字母所代表的正方形的面积为144的选项为( )
A、 |
B、 |
C、 |
D、 |