题目内容
4.某商场计划用500元购进A型节能台灯,用3000元购进B型节能台灯,已知A型节能台灯的进货单价比B型的进货单价少20元.(1)若B型节能灯购进的数量是A型数量的3倍,这两种台灯各购进多少盏?
(2)若A型节能灯的进价为20元/盏,售价为35元/盏,B型节能灯的售价为60元/盏,商场购进100盏台灯且规定B型台灯的进货数量不超过A型台灯数量的2倍,应怎样进货才能使商场在销售完这批台灯时获利最多?此时利润为多少元?
分析 (1)设A型台灯购进x盏,则B型台灯购进3x盏,根据A型节能台灯的进货单价比B型的进货单价少20元,列方程求解;
(2)设购进B型台灯m盏,根据商场购进100盏台灯且规定B型台灯的进货数量不超过A型台灯数量的2倍,列不等式求解,进一步得到商场在销售完这批台灯时获利最多时的利润.
解答 解:(1)设A型台灯购进x盏,则B型台灯购进3x盏,依题意有
$\frac{500}{x}$+20=$\frac{3000}{3x}$,
解得:x=25.
经检验,x=25是原方程的解,
3x=3×25=75.
故A型台灯购进25盏,则B型台灯购进75盏.
(2)设购进B型台灯m盏,依题意有
m≤2(100-m),
解得m≤66$\frac{2}{3}$,
35-20=15(元),
60-(20+20)=20(元),
∵m为整数,15<20,
∴m=66,即A型台灯购进34盏,B型台灯购进66盏时获利最多,
34×15+20×66
=510+1320
=1830(元).
此时利润为1830元.
点评 本题考查了分式方程的应用和一元一次不等式的应用,解答本题的关键是读懂题意,找出合适的等量关系和不等关系,列方程和不等式求解.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
9.估计$\sqrt{9}$×$\sqrt{\frac{1}{3}}$+$\sqrt{12}$的运算结果应在哪两个连续自然数之间( )
| A. | 5和6 | B. | 6和7 | C. | 7和8 | D. | 8和9 |
14.某自行车厂一周计划生产1050辆自行车,平均每天生产150辆,由于各种原因实际每天生产量与计划量相比有出入,下表是某周的生产情况(超产为正,减产为负):
(1)根据记录可知前三天共生产449辆;
(2)产量最多的一天比产量最少的一天多生产26辆;
(3)该厂实行计件工资制,每辆车50元,一周若超额完成任务则超额部分每辆另奖10元,若完不成任务,则少生产一辆倒扣10元,那么该厂工人这一周的工资总额是多少?
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
(2)产量最多的一天比产量最少的一天多生产26辆;
(3)该厂实行计件工资制,每辆车50元,一周若超额完成任务则超额部分每辆另奖10元,若完不成任务,则少生产一辆倒扣10元,那么该厂工人这一周的工资总额是多少?
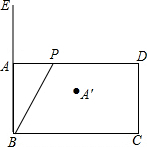 如图,矩形ABCD中,AB=2,BC=2$\sqrt{3}$,动点P从A点出发,沿AD运动到D点,连接BP,点A关于直线BP的对称点为A′,
如图,矩形ABCD中,AB=2,BC=2$\sqrt{3}$,动点P从A点出发,沿AD运动到D点,连接BP,点A关于直线BP的对称点为A′,