Question

12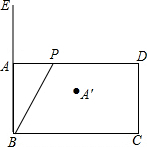．如图，矩形ABCD中，AB=2，BC=2$\sqrt{3}$，动点P从A点出发，沿AD运动到D点，连接BP，点A关于直线BP的对称点为A′，
（1）在整个运动过程中，点A′所经过的路径的长为$\frac{4}{3}$π；
（2）点E在BA的延长线上，EA=2，直线l经过点E，与直线EA所夹锐角为α，若点A′有2次机会落在直线l上，则tanα的取值范围是0＜tanα＜$\frac{\sqrt{3}}{3}$．

Answer 1

分析 （1）由图象可知，点A′的运动轨迹是以B为圆心，BA为半径的圆弧，当P与D重合时，∠ABA′=2∠ABD=120°，利用弧长公式计算即可；
（2）设$\widehat{AA°}$交BD于K．作直线EK，易证EK是⊙B的切线，可以推出∠BEK=30°，所以当α＜30°时，若点A′有2次机会落在直线l上，由此即可解决问题；

解答 解：（1）如图，连接BD．
∵四边形ABCD是矩形，
∴∠BAD=90°，
∴AB=2，AD=2$\sqrt{3}$，
∴tan∠ABD=$\frac{AD}{AB}$=$\sqrt{3}$，
∴∠ABD=60°，
由图象可知，点A′的运动轨迹是以B为圆心，BA为半径的圆弧，当P与D重合时，∠ABA′=2∠ABD=120°，
∴点A′所经过的路径的长为$\frac{120π•2}{180}$=$\frac{4}{3}$π，
故答案为$\frac{4}{3}$π．

（2）设$\widehat{AA′}$交BD于K．作直线EK，易证EK是⊙B的切线，
∴∠EKB=90°，
∵∠EBK=60°，
∴∠BEK=30°，
∴当α＜30°时，若点A′有2次机会落在直线l上，
∴tanα的取值范围是0＜tanα＜$\frac{\sqrt{3}}{3}$，
故答案为0＜tanα＜$\frac{\sqrt{3}}{3}$．

点评 本题考查轨迹、矩形的性质、锐角三角函数、切线的判定和性质等知识，解题的关键是正确寻找点A′的运动轨迹，学会利用特殊位置解决问题，所以中考常考题型．