题目内容
13.抛物线y=x2-ax+a-2与x轴交于点(-1,0),则抛物线y=ax2+2x的开口向上.分析 首先根据抛物线y=x2-ax+a-2与x轴交于点(-1,0)求出a的值,进而根据二次函数的性质确定抛物线的开口方向.
解答 解:∵抛物线y=x2-ax+a-2与x轴交于点(-1,0),
∴0=1+a+a-2,
∴a=$\frac{1}{2}$,
∴抛物线y=$\frac{1}{2}$x2+2x的开口向上,
故答案为上.
点评 本题主要考查了抛物线与x轴的交点与二次函数的性质,解题的关键是求出a的值,此题难度不大.

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
8.抛物线y=4(x-3)2+2的顶点坐标是( )
| A. | (3,-2) | B. | (3,2) | C. | (-3,-2) | D. | (-3,2) |





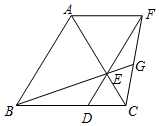 如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、CF,联结BE并延长交CF于点G
如图,已知△ABC是等边三角形,点D、E分别在边BC、AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF、CF,联结BE并延长交CF于点G