题目内容
2. 如图所示,正方形ABCD的面积为6,AE=2ED且EF=3FC,求三角形ABF的面积?
如图所示,正方形ABCD的面积为6,AE=2ED且EF=3FC,求三角形ABF的面积?
分析 过F作MN∥BC,交AB于M,交CD于N,由条件可求得FN与FM的关系,利用正方形的面积,可求得正方形的边长,则可求得FM的长,可求得答案.
解答  解:
解:
如图,过F作MN∥BC,交AB于M,交CD于N,
∵EF=3FC,
∴$\frac{FN}{DE}$=$\frac{FC}{EC}$=$\frac{FC}{EF+FC}$=$\frac{FC}{4FC}$=$\frac{1}{4}$,即DE=4FN,
∵AE=2ED,
∴AE=8FN,
∴AD=12FN,
∵正方形面积为6,
∴AD=MN=AB=$\sqrt{6}$,
∴FN=$\frac{\sqrt{6}}{12}$,
∴FM=$\frac{11\sqrt{6}}{12}$,
∴S△ABF=$\frac{1}{2}$AB•FM=$\frac{1}{2}$×$\sqrt{6}$×$\frac{11\sqrt{6}}{12}$=$\frac{11}{4}$.
点评 本题主要考查正方形的性质,利用条件找到FN与AD的关系是解题的关键.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
4.依法纳税是公民应尽的义务.根据新税法,2008年3月开始将执行新的起征点,个人所得税起征点自2008年3月1日起由1600元提高到2000元,即公民全月工资薪金所得不超过2000元不必纳税,超过2000元的部分为全月应纳税所得额.此项税款按下表累加计算:
(1)根据上表,填空:
(2)2009年4月王娟的工资薪金比李丽的工资薪金多100元,她们该月的纳税总金额是25元,求该月王娟和李丽的工资薪金各是多少元?
| 级数 | 全月应纳税所得额 | 税率% |
| 1 | 不超过500元的部分 | 5 |
| 2 | 超过500元至2000元的部分 | 10 |
| 3 | 超过2000元至5000元的部分 | 15 |
| 4 | 超过5000元至20000元的部分 | 20 |
| … | … |
| 公民 | 工资薪金(元) | 应纳税金(元) |
| 甲 | 2000 | 0 |
| 乙 | 2500 | 25 |
| 丙 | 3900 | 165 |
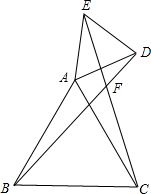 已知:如图所示,△ABC与△ADE均为等边三角形,点A为它们公共顶点,现连接BD、EC,BD与EC交于F点:
已知:如图所示,△ABC与△ADE均为等边三角形,点A为它们公共顶点,现连接BD、EC,BD与EC交于F点: