题目内容
3.观察下列各式,回答问题1-$\frac{1}{{2}^{2}}$=$\frac{1}{2}$×$\frac{3}{2}$,1-$\frac{1}{{3}^{2}}$=$\frac{2}{3}$×$\frac{4}{3}$,1-$\frac{1}{{4}^{2}}$=$\frac{3}{4}$×$\frac{5}{4}$….
按上述规律填空:
(1)1-$\frac{1}{10{0}^{2}}$=$\frac{99}{100}$×$\frac{101}{100}$.
(2)计算:(1-$\frac{1}{{2}^{2}}$)×(1-$\frac{1}{{3}^{2}}$)×…×(1-$\frac{1}{200{4}^{2}}$)×(1-$\frac{1}{200{5}^{2}}$)=$\frac{1003}{2005}$.
分析 (1)观察已知等式确定出所求即可;
(2)原式根据题中的规律化简,计算即可得到结果.
解答 解:(1)1-$\frac{1}{10{0}^{2}}$=$\frac{99}{100}$×$\frac{101}{100}$;
(2)原式=$\frac{1}{2}$×$\frac{3}{2}$×$\frac{2}{3}$×$\frac{4}{3}$×$\frac{3}{4}$×$\frac{5}{4}$×…×$\frac{2003}{2004}$×$\frac{2005}{2004}$×$\frac{2004}{2005}$×$\frac{2006}{2005}$=$\frac{1}{2}$×$\frac{2006}{2005}$=$\frac{1003}{2005}$.
故答案为:(1)$\frac{99}{100}$;$\frac{101}{100}$;(2)$\frac{1003}{2005}$
点评 此题考查了有理数的混合运算,弄清题中的规律是解本题的关键.

练习册系列答案
相关题目
19.下列命题正确的是( )
| A. | 对角线相等且互相平分的四边形是矩形 | |
| B. | 对角线互相垂直的四边形是菱形 | |
| C. | 菱形的面积等于对角线的积 | |
| D. | 平行四边形每条对角线平分一组对角 |
20.关于?ABCD的叙述,正确的是( )
| A. | 若AB⊥BC,则?ABCD是菱形 | B. | 若AC⊥BD,则?ABCD是正方形 | ||
| C. | 若AC=BD,则?ABCD是矩形 | D. | 若AB=AD,则?ABCD是正方形 |
17.下列二次根式是最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\sqrt{10}$ | C. | $\sqrt{12}$ | D. | $\sqrt{18}$ |
4.-$\sqrt{3}$是$\sqrt{3}$的( )
| A. | 绝对值 | B. | 平方根 | C. | 算术平方根 | D. | 相反数 |
8.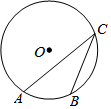 已知如图$\widehat{AB}$:$\widehat{ACB}$=1:5,则∠ACB的度数( )
已知如图$\widehat{AB}$:$\widehat{ACB}$=1:5,则∠ACB的度数( )
 已知如图$\widehat{AB}$:$\widehat{ACB}$=1:5,则∠ACB的度数( )
已知如图$\widehat{AB}$:$\widehat{ACB}$=1:5,则∠ACB的度数( )| A. | 30° | B. | 35° | C. | 40° | D. | 60° |
15.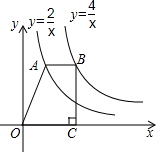 如图,点A在函数y=$\frac{2}{x}$(x>0)的图象上,点B在函数y=$\frac{4}{x}$(x>0)的图象上,且AB∥x轴,BC⊥x轴于点C,则四边形ABCO的面积为( )
如图,点A在函数y=$\frac{2}{x}$(x>0)的图象上,点B在函数y=$\frac{4}{x}$(x>0)的图象上,且AB∥x轴,BC⊥x轴于点C,则四边形ABCO的面积为( )
 如图,点A在函数y=$\frac{2}{x}$(x>0)的图象上,点B在函数y=$\frac{4}{x}$(x>0)的图象上,且AB∥x轴,BC⊥x轴于点C,则四边形ABCO的面积为( )
如图,点A在函数y=$\frac{2}{x}$(x>0)的图象上,点B在函数y=$\frac{4}{x}$(x>0)的图象上,且AB∥x轴,BC⊥x轴于点C,则四边形ABCO的面积为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
13.$\sqrt{7}$ 是一个无理数,请估计$\sqrt{7}$在哪两个整数之间?( )
| A. | 1与2 | B. | 2与3 | C. | 3与4 | D. | 4与5 |