题目内容
18. 如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m,如果梯子的顶端下滑1m,那么梯子的底端滑动($\sqrt{51}$-6)m.
如图,一个长为10m的梯子斜靠在墙上,梯子的顶端距地面的垂直距离为8m,如果梯子的顶端下滑1m,那么梯子的底端滑动($\sqrt{51}$-6)m.
分析 已知AB,AO,在直角△ABO中即可计算BO,梯子的顶端下滑1米,即CO=7米,CD=AB=10米,在直角△COD中,根据勾股定理即可计算OD,底端滑动的距离为OD-OB,计算即可.
解答 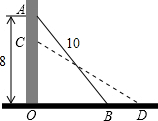 解:在△AOB中,∠AOB=90°,AB=10米,AO=8米,由勾股定理得OB=6米,
解:在△AOB中,∠AOB=90°,AB=10米,AO=8米,由勾股定理得OB=6米,
△COD中,∠C=90°,AB=10米,CO=7米,由勾股定理得OD=$\sqrt{1{0}^{2}-{7}^{2}}$=$\sqrt{51}$米,
∴BD=OD-OB=$\sqrt{51}$-6(米),
∴梯子底端滑动($\sqrt{51}$-6)米.
故答案为($\sqrt{51}$-6).
点评 本题考查了勾股定理在实际生活中的应用,本题中根据梯子长不会变的等量关系求解是解题的关键.

练习册系列答案
 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
8.代数式-6xy3的系数与次数分别是( )
| A. | -2,4 | B. | -6,3 | C. | -2,3 | D. | -6,4 |
6. 如图,点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,OA=10,OA′=20,则五边形ABCDE的面积与五边形A′B′C′D′E′的面积的比值是( )
如图,点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,OA=10,OA′=20,则五边形ABCDE的面积与五边形A′B′C′D′E′的面积的比值是( )
 如图,点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,OA=10,OA′=20,则五边形ABCDE的面积与五边形A′B′C′D′E′的面积的比值是( )
如图,点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,OA=10,OA′=20,则五边形ABCDE的面积与五边形A′B′C′D′E′的面积的比值是( )| A. | 2:1 | B. | 1:2 | C. | 4:1 | D. | 1:4 |
3.若a、b为倒数,c、d互为相反数,则代数式4ab-c-d的值是( )
| A. | -3 | B. | 3 | C. | 4 | D. | -4 |
8. 如图1是边长为20cm的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
如图1是边长为20cm的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
(1)请帮小明在图1中用虚线画出折痕;
(2)设剪去的小正方形的边长为x(cm),折成的长方体盒子的容积为V(cm3),用只含字母x的式子表示这个盒子的高为xcm,底面积为(20-2x)2cm2,盒子的容积V为x(20-2x)2cm3;
(3)为探究盒子的体积与剪去的小正方形的边长x之间的关系,小明列表分析:
请将表中数据补充完整,并根据表格中的数据写出当x的值逐渐增大时,V的值如何变化?
 如图1是边长为20cm的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).
如图1是边长为20cm的正方形薄铁片,小明将其四角各剪去一个相同的小正方形(图中阴影部分)后,发现剩余的部分能折成一个无盖的长方体盒子,图2为盒子的示意图(铁片的厚度忽略不计).(1)请帮小明在图1中用虚线画出折痕;
(2)设剪去的小正方形的边长为x(cm),折成的长方体盒子的容积为V(cm3),用只含字母x的式子表示这个盒子的高为xcm,底面积为(20-2x)2cm2,盒子的容积V为x(20-2x)2cm3;
(3)为探究盒子的体积与剪去的小正方形的边长x之间的关系,小明列表分析:
| x(cm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| V(cm3) | 324 | 512 | 588 | 576 | 500 | 384 | 252 | 128 |
 已知抛物线的顶点为(2,-1),且过(1,0)点.
已知抛物线的顶点为(2,-1),且过(1,0)点.