题目内容
12.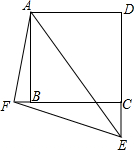 如图.在正方形ABCD中,点E,F分别为DC,CB延长线上的点.且满足∠EAF=45°,∠BAF=15°,连接EF,求证:DE-BF=EF.
如图.在正方形ABCD中,点E,F分别为DC,CB延长线上的点.且满足∠EAF=45°,∠BAF=15°,连接EF,求证:DE-BF=EF.
分析 在DE上取一点G,使DG=BF,根据正方形的性质求出∠D=∠ABC=∠ABF=90°,然后利用“边角边”证明△ABF和△ADG全等,根据全等三角形对应角相等可得,∠DAG=∠BAF=15°,全等三角形对应边相等可得AG=AF,然后求出∠BAE的度数以及∠GAE的度数,根据度数求出∠GAE=∠FAE=45°,再利用“边角边”证明△AFE和△AGE全等,根据全等三角形对应边相等可得EF=GE,然后根据图形边的关系进行等量代换即可得解.
解答 证明:在DE上取一点G,使DG=BF, 在正方形ABCD中,AD=AB,∠D=∠ABC=∠ABF=90°,
在正方形ABCD中,AD=AB,∠D=∠ABC=∠ABF=90°,
在△ABF和△ADG中,
$\left\{\begin{array}{l}{DG=BF}\\{∠D=∠ABF=90°}\\{AD=AB}\end{array}\right.$,
∴△ABF≌△ADG(SAS),
∴∠DAG=∠BAF=15°,AG=AF,
∵∠EAF=45°,∠BAF=15°,
∴∠BAE=∠EAF-∠BAF=45°-15°=30°,
∴∠GAE=90°-15°-30°=45°,
∴∠GAE=∠FAE=45°,
在△AFE和△AGE中,
$\left\{\begin{array}{l}{AG=AF}\\{∠GAE=∠FAE=45°}\\{AE=AE}\end{array}\right.$,
∴△AFE≌△AGE(SAS),
∴EF=GE,
∴EF+BF=EG+DG=DE,
∴DE-BF=EF.
点评 本题考查了正方形的性质,全等三角形的判定与性质,题目比较复杂,需要利用二次全等进行证明,作辅助线构造出全等三角形是解题的关键.

练习册系列答案
相关题目
1.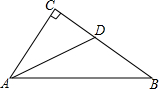 如图,在△ABC中,∠C=90°,∠CAB的平分线交BC于点D,若AB=5,AC=3,则△DAB的面积为( )
如图,在△ABC中,∠C=90°,∠CAB的平分线交BC于点D,若AB=5,AC=3,则△DAB的面积为( )
 如图,在△ABC中,∠C=90°,∠CAB的平分线交BC于点D,若AB=5,AC=3,则△DAB的面积为( )
如图,在△ABC中,∠C=90°,∠CAB的平分线交BC于点D,若AB=5,AC=3,则△DAB的面积为( )| A. | 3 | B. | $\frac{15}{4}$ | C. | 5 | D. | $\frac{25}{8}$ |
 如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,那么S3=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)3,则Sn=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.(用含n的式子表示)
如图,正△ABC的边长为2,以BC边上的高AB1为边作正△AB1C1,△ABC与△AB1C1公共部分的面积记为S1;再以正△AB1C1边B1C1上的高AB2为边作正△AB2C2,△AB1C1与△AB2C2公共部分的面积记为S2;…,以此类推,那么S3=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)3,则Sn=$\frac{\sqrt{3}}{2}$($\frac{3}{4}$)n.(用含n的式子表示) 初三某班学生去中央公园踏青,班级信息员骑自行车先从学校出发,5分钟后其余同学以60米/分的速度从学校向公园行进,信息员先到达公园后用5分钟找到聚集地点,再立即按原路以另一速度返回到队伍汇报聚集地点,最后与同学们一起步行到公园,信息员离其余同学的距离y(米)与信息员出发的时间x(分)之间的关系如图所示,则信息员开始返回之后,再经过3分钟与其余同学相距720米.
初三某班学生去中央公园踏青,班级信息员骑自行车先从学校出发,5分钟后其余同学以60米/分的速度从学校向公园行进,信息员先到达公园后用5分钟找到聚集地点,再立即按原路以另一速度返回到队伍汇报聚集地点,最后与同学们一起步行到公园,信息员离其余同学的距离y(米)与信息员出发的时间x(分)之间的关系如图所示,则信息员开始返回之后,再经过3分钟与其余同学相距720米.