题目内容
19.下列各等式:①$\sqrt{(-2)^{2}}$=-2;②(-$\sqrt{2}$)2=2;③$\sqrt{(-2)^{-2}}$=$\frac{1}{2}$;④(-$\sqrt{2}$)-2=$\frac{1}{2}$;⑤-$\sqrt{(-2)^{2}}$=2;⑥(-$\sqrt{-2}$)2=2,其中成立的是②③④(填序号).分析 根据算术平方根和负整数指数幂的定义分别对每一项进行分析,即可得出答案.
解答 解:∵①$\sqrt{(-2)^{2}}$=2;⑤-$\sqrt{(-2)^{2}}$=-2;⑥(-$\sqrt{-2}$)2无意义,
∴成立的是②③④;
故答案为:②③④.
点评 此题考查了算术平方根和负整数指数幂,熟练掌握定义是解题的关键,是一道基础题.

练习册系列答案
相关题目
1.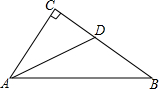 如图,在△ABC中,∠C=90°,∠CAB的平分线交BC于点D,若AB=5,AC=3,则△DAB的面积为( )
如图,在△ABC中,∠C=90°,∠CAB的平分线交BC于点D,若AB=5,AC=3,则△DAB的面积为( )
 如图,在△ABC中,∠C=90°,∠CAB的平分线交BC于点D,若AB=5,AC=3,则△DAB的面积为( )
如图,在△ABC中,∠C=90°,∠CAB的平分线交BC于点D,若AB=5,AC=3,则△DAB的面积为( )| A. | 3 | B. | $\frac{15}{4}$ | C. | 5 | D. | $\frac{25}{8}$ |
14. 有这样一个问题:探究函数y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x的性质.
有这样一个问题:探究函数y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x的性质.
(1)先从简单情况开始探究:
①当函数y=$\frac{1}{2}$(x-1)+x时,y随x增大而增大(填“增大”或“减小”);
②当函数y=$\frac{1}{2}$(x-1)(x-2)+x时,它的图象与直线y=x的交点坐标为(1,1),(2,2);
(2)当函数y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x时,
下表为其y与x的几组对应值.
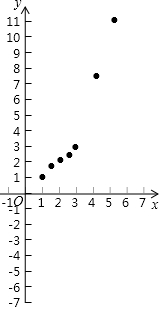
①如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,请根据描出的点,画出该函数的图象;
②根据画出的函数图象,写出该函数的一条性质:y随x的增大而增大.
 有这样一个问题:探究函数y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x的性质.
有这样一个问题:探究函数y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x的性质.(1)先从简单情况开始探究:
①当函数y=$\frac{1}{2}$(x-1)+x时,y随x增大而增大(填“增大”或“减小”);
②当函数y=$\frac{1}{2}$(x-1)(x-2)+x时,它的图象与直线y=x的交点坐标为(1,1),(2,2);
(2)当函数y=$\frac{1}{2}$(x-1)(x-2)(x-3)+x时,
下表为其y与x的几组对应值.
| x | … | -$\frac{1}{2}$ | 0 | 1 | $\frac{3}{2}$ | 2 | $\frac{5}{2}$ | 3 | 4 | $\frac{9}{2}$ | … |
| y | … | -$\frac{113}{16}$ | -3 | 1 | $\frac{27}{16}$ | 2 | $\frac{37}{16}$ | 3 | 7 | $\frac{177}{16}$ | … |
②根据画出的函数图象,写出该函数的一条性质:y随x的增大而增大.
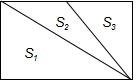 如图是由三个三角形组成的一个面积为(6a2+4a)cm2的长方形,三个三角形的面积分别是S1,S2,S3,若S1=(3a2+2a)cm2,S3=(2a2-a)cm2,则S2等于(a2+3a)cm2.
如图是由三个三角形组成的一个面积为(6a2+4a)cm2的长方形,三个三角形的面积分别是S1,S2,S3,若S1=(3a2+2a)cm2,S3=(2a2-a)cm2,则S2等于(a2+3a)cm2. 如图,∠3和∠9是直线AD、BD被直线AC所截而成的同位角;∠6和∠9是直线BC、AC被直线BD所截而成的同位角.
如图,∠3和∠9是直线AD、BD被直线AC所截而成的同位角;∠6和∠9是直线BC、AC被直线BD所截而成的同位角.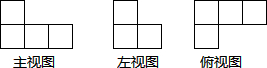 在一个仓库里堆放有若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画出来,如图,则这堆货箱共有5个.
在一个仓库里堆放有若干个相同的正方体货箱,仓库管理员将这堆货箱的三视图画出来,如图,则这堆货箱共有5个.