题目内容
11.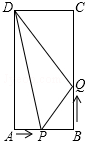 如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动.
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动.(1)问几秒后△PBQ的面积等于8cm2?
(2)是否存在这样的时刻,使S△PDQ=8cm2,试说明理由.
分析 (1)设x秒后△PBQ的面积等于8cm2,用含x的代数式分别表示出PB,QB的长,再利用△PBQ的面积等于8列式求值即可;
(2)假设存在t使得△PDQ面积为8cm2,根据△PDQ的面积等于8cm2列式计算即可.
解答 解:(1)设x秒后△PBQ的面积等于8cm2.
∵AP=x,QB=2x.
∴PB=6-x.
∴$\frac{1}{2}$×(6-x)2x=8,
解得x1=2,x2=4,
答:2秒或4秒后△PBQ的面积等于8cm2
(2)设出发秒x时△DPQ的面积等于8cm2.
∵S矩形ABCD-S△APD-S△BPQ-S△CDQ=S△DPQ
∴12×6-$\frac{1}{2}$×12x-$\frac{1}{2}$×2x(6-x)-$\frac{1}{2}$×6×(12-2x)=8,
化简整理得 x2-6x+28=0,
∵△=36-4×28=-76<0,
∴原方程无解,
∴不存在这样的时刻,使S△PDQ=8cm2.
点评 此题考查一元二次方程的应用;表示出所给三角形的两条直角边长是解决本题的突破点;用到的知识点为:直角三角形的面积=两直角边积的一半,矩形的面积=长×宽.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
3. 数轴上与1的距离等于2个单位的点表示的数是( )
数轴上与1的距离等于2个单位的点表示的数是( )
 数轴上与1的距离等于2个单位的点表示的数是( )
数轴上与1的距离等于2个单位的点表示的数是( )| A. | 0和2 | B. | -1和2 | C. | -1和3 | D. | -2和2 |
20.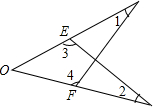 如图,∠1=∠2,3=∠4,OE=OF,则图中全等三角形有( )
如图,∠1=∠2,3=∠4,OE=OF,则图中全等三角形有( )
 如图,∠1=∠2,3=∠4,OE=OF,则图中全等三角形有( )
如图,∠1=∠2,3=∠4,OE=OF,则图中全等三角形有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
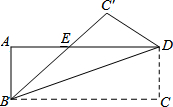 如图,长方形ABCD中,AB=4,BC=8,将长方形沿BC折叠,点C落在C′处.△BDE的面积是多少?
如图,长方形ABCD中,AB=4,BC=8,将长方形沿BC折叠,点C落在C′处.△BDE的面积是多少? 已知a、b、c三个数在数轴上对应点的位置如图所示,下列几个判断:①a<c<b;②-a<b;③a+b>0;④c-a<0中,错误的个数是( )
已知a、b、c三个数在数轴上对应点的位置如图所示,下列几个判断:①a<c<b;②-a<b;③a+b>0;④c-a<0中,错误的个数是( )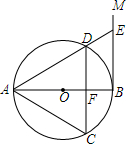 如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且DA=DC,链接AC,AD,延长AD交BM地点E.
如图,AB是⊙O的直径,过点B作⊙O的切线BM,弦CD∥BM,交AB于点F,且DA=DC,链接AC,AD,延长AD交BM地点E.