题目内容
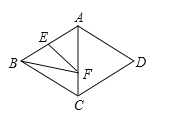
【题目】两把大小不同、含30度角的三角板如图放置，如图，若AO＝2，点N在线段OD上，且NO＝1，点P是线段AB上的一个动点，将△COD固定，△AOB绕点O逆时针旋转的过程中，线段PN长度的最大值是_____；最小值是_____．
【答案】2
+1 ﹣1
【解析】
过O作OE⊥AB于E，由已知条件求出当P在点E处时，点P到O点的距离最近为 ，当旋转到OE与OD重合可得NP的最小值；当点P在点B处时，且当旋转到OB在DO的延长线时，可得NP的最大值OB+ON．
解：如图1，过O作OE⊥AB于E，
∵AO＝2，∠ABO＝30°，
∴AB＝4，OB＝
∴
∴
∴当P在点E处时，点P到O点的距离最近为，
这时当旋转到OE与OD重合是，NP取最小值为：OP﹣ON＝﹣1，
如图2，当点P在点B处时，且当旋转到OB在DO的延长线时，
NP取最大值OB+ON＝2+1，
∴线段PN长度的最大值为
，最小值为
，
故答案为：，．
练习册系列答案
相关题目
