Question

【题目】如图，点P为正方形ABCD的对角线AC上的一点，连接BP并延长交CD于点E，交AD的延长线于点F，⊙O是△DEF的外接圆，连接DP．

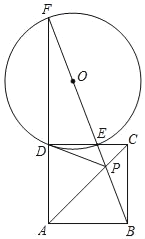
（1）求证：DP是⊙O的切线；

（2）若tan∠PDC＝，正方形ABCD的边长为4，求⊙O的半径和线段OP的长．

Answer 1

【答案】（1）见解析；（2）⊙O的半径，.

【解析】

（1）连接OD，可证△CDP≌△CBP，可得∠CDP=∠CBP，由∠CBP+∠BEC=90°，∠BEC=∠OED=∠ODE，可证出∠ODP=90°，则DP是⊙O的切线；

（2）先求出CE长，在Rt△DEF中可求出EF长，证明△DPE∽△FPD，由比例线段可求出EP长，则OP可求出．

解：（1）连接OD，

∵正方形ABCD中，CD＝BC，CP＝CP，∠DCP＝∠BCP＝45°，

∴△CDP≌△CBP（SAS），

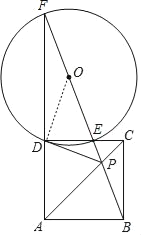
∴∠CDP＝∠CBP，

∵∠BCD＝90°，

∴∠CBP+∠BEC＝90°，

∵OD＝OE，

∴∠ODE＝∠OED，

又∵∠OED＝∠BEC，

∴∠BEC＝∠OED＝∠ODE，

∴∠CDP+∠ODE＝90°，

∴∠ODP＝90°，

∴DP是⊙O的切线；

（2）∵∠CDP＝∠CBE，

∴tan，

∴CE＝，

∴DE＝2，

∵∠EDF＝90°，

∴EF是⊙O的直径，

∴∠F+∠DEF＝90°，

∴∠F＝∠CDP，

在Rt△DEF中，，

∴DF＝4，

∴＝＝2，

∴，

∵∠F＝∠PDE，∠DPE＝∠FPD，

∴△DPE∽△FPD，

∴，

设PE＝x，则PD＝2x，

∴，

解得x＝，

∴OP＝OE+EP＝．