题目内容
18.设m、n是方程x2-2x-3=0的二个实数根,则m2+n2-2m-2n=6.分析 利用根与系数的关系及一元二次方程的解的定义得出m+n=2,m•n=-3,m2=3+2m,n2=3+2n,再将m2+n2-2m-2n=变形为两根之积或两根之和的形式,然后代入数值计算即可.
解答 解:∵m、n是方程x2-2x-3=0的两个实数根,
∴mn=-3,m+n=2,m2-2m-3=0,
∴m2=3+2m,n2=3+2n,
∴m2+n2-2m-2n=3+2m+3+2n-2m-2n=6,
故答案为:6.
点评 此题主要考查了根与系数的关系及一元二次方程的解的定义,将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
8.如图,是一个几何体的三视图,则这几何体的表面积是( )
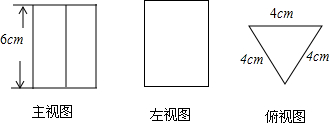

| A. | 72cm2 | B. | 60cm2 | C. | (72+4$\sqrt{3}$)cm2 | D. | (72+8$\sqrt{3}$)cm2 |
13.下面的方程中是一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | (x+1)(x-1)=x2-1 | C. | x2=-1 | D. | x2+y=5 |
3.下列方程中,是关于x的一元二次方程的是( )
| A. | 3(x+1)2=2(x+1) | B. | $\frac{1}{x^2}+\frac{1}{x}-2=0$ | C. | ax2+bx+c=0 | D. | 2x=1 |
10.下列图形中有稳定性的是( )
| A. | 正方形 | B. | 直角三角形 | C. | 长方形 | D. | 平行四边形 |
7.下列说法中:①如果两个三角形可以依据“AAS”来判定全等,那么一定也可以依据“ASA”来判定它们全等;②如果两个三角形都和第三个三角形不全等,那么这两个三角形也不一定全等;③如果两个等腰三角形的腰和一个内角分别对应相等,那么这两个等腰三角形一定全等;④要判断两个三角形全等,给出的条件中至少要有一组边对应相等.正确的是( )
| A. | ①②④ | B. | ②③④ | C. | ①③④ | D. | ①②③ |
8.下列运算正确的是( )
| A. | -$\frac{5}{7}$+$\frac{2}{7}$=-($\frac{5}{7}$+$\frac{2}{7}$) | B. | (-2$\frac{1}{3}$)3=-8$\frac{1}{27}$ | ||
| C. | 3÷$\frac{5}{4}$×$\frac{4}{5}$=3÷1=3 | D. | 3$\frac{1}{4}$×(-3.25)-6$\frac{3}{4}$×3.25=-32.5 |