题目内容
14.实数m,n满足2m-n2=4,则y=m2+2n2+4m+1的最小值是13.分析 把2m-n2=4变形为n2=2m-4,代入函数关系式,运用配方法把解析式化为顶点式,求出最小值即可.
解答 解:∵2m-n2=4,∴2m=n2+4,
∴m的最小值是2,
∵2m-n2=4,∴n2=2m-4,
∴y=m2+2n2+4m+1
=m2+4m-8+4m+1
=(m+4)2-23,
∴当m=2时,y的最小值是13,
故答案为:13.
点评 本题考查的是二次函数的最小值的确定,掌握配方法的一般步骤是解题的关键.

练习册系列答案
相关题目
19.若二次根式$\sqrt{2x-4}$有意义,则x的取值范围是( )
| A. | x=2 | B. | x≠2 | C. | x≤2 | D. | x≥2 |
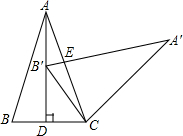 如图,在△ABC中,AB=AC=6,AD⊥BC,D为垂足,将△ABC绕点C顺时针旋转,点B落在线段AD上的点B′处,A′B′交AC于E,∠B=75°,那么B′E的长为6-3$\sqrt{3}$.
如图,在△ABC中,AB=AC=6,AD⊥BC,D为垂足,将△ABC绕点C顺时针旋转,点B落在线段AD上的点B′处,A′B′交AC于E,∠B=75°,那么B′E的长为6-3$\sqrt{3}$.
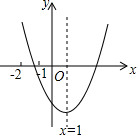 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,现有下列结论: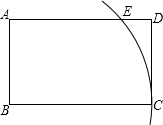 如图,在矩形ABCD中,AB=3,BC=5,以点B为圆心,BC长为半径画弧,交边AD于点E,则AE•ED=4.
如图,在矩形ABCD中,AB=3,BC=5,以点B为圆心,BC长为半径画弧,交边AD于点E,则AE•ED=4.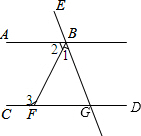 如图,已知AB∥CD,∠1:∠2=1:2,∠2:∠3=2:3,求∠1、∠2、∠3的度数.
如图,已知AB∥CD,∠1:∠2=1:2,∠2:∠3=2:3,求∠1、∠2、∠3的度数.