题目内容
7.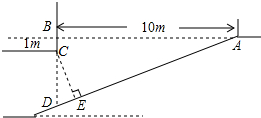 近年来,有私家车的业主越来越多,某小区为解决“停车难”问题,拟建造一个地下停车库.如图是该地下停车库坡道入口的设计示意图,其中水平线AB=10m,BD⊥AB,∠BAD=20°,点C在BD上,BC=1m.根据规定,地下停车库坡道入口上方要张贴限高标志,以提醒驾驶员所驾车辆能否安全驶入.李建认为CD的长度就是限制的高度,而孙杰认为应该以CE的长度作为限制的高度.李建和孙杰谁说的对?请你判断并计算出限制高度.(结果精确到0.1m,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
近年来,有私家车的业主越来越多,某小区为解决“停车难”问题,拟建造一个地下停车库.如图是该地下停车库坡道入口的设计示意图,其中水平线AB=10m,BD⊥AB,∠BAD=20°,点C在BD上,BC=1m.根据规定,地下停车库坡道入口上方要张贴限高标志,以提醒驾驶员所驾车辆能否安全驶入.李建认为CD的长度就是限制的高度,而孙杰认为应该以CE的长度作为限制的高度.李建和孙杰谁说的对?请你判断并计算出限制高度.(结果精确到0.1m,参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)
分析 根据锐角三角函数关系得出BD以及CD的长,进而得出EC的长即可得出答案.
解答 解:孙杰说的对.
在△ABD中,∠ABD=90°,∠BAD=20°,AB=10°,
∴tan∠BAD=$\frac{BD}{AB}$,
∴BD=10×tan 20≈10×0.36=3.6(m),
∴CD=BD-BC≈3.6-1=2.6(m),
在△CDE中,∠CDE=90°-∠BAD=70°.
又∵CE⊥ED,
∴∠DCE=90°-70°=20°,
∴cos∠DCE=$\frac{CE}{CD}$,
∴CE=CD×cos∠DCE≈2.6×cos20°≈2.6×0.94≈2.4(m).
答:地下停车库坡道入口限制高度约为2.4m.
点评 此题主要考查了解直角三角形的应用,根据题意熟练应用锐角三角函数关系是解题关键.

练习册系列答案
相关题目
17.9的算术平方根是( )
| A. | ±81 | B. | 81 | C. | ±3 | D. | 3 |
2.数据3,5,1,7的平均数和方差分别是( )
| A. | 5,2 | B. | 3,5 | C. | 4,20 | D. | 4,5 |
19. 如图,已知AB∥CD,∠DFE=130°,则∠ABE的度数为( )
如图,已知AB∥CD,∠DFE=130°,则∠ABE的度数为( )
 如图,已知AB∥CD,∠DFE=130°,则∠ABE的度数为( )
如图,已知AB∥CD,∠DFE=130°,则∠ABE的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 130° |
1.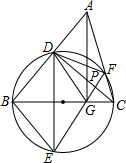 如图,在锐角△ABC中,以BC为直径的圆分别交AB,AC于点D,F.若E,D关于BC对称,连接EF交BC于点G,AG与CD相交于点P,则点P一定为△DFG的( )
如图,在锐角△ABC中,以BC为直径的圆分别交AB,AC于点D,F.若E,D关于BC对称,连接EF交BC于点G,AG与CD相交于点P,则点P一定为△DFG的( )
 如图,在锐角△ABC中,以BC为直径的圆分别交AB,AC于点D,F.若E,D关于BC对称,连接EF交BC于点G,AG与CD相交于点P,则点P一定为△DFG的( )
如图,在锐角△ABC中,以BC为直径的圆分别交AB,AC于点D,F.若E,D关于BC对称,连接EF交BC于点G,AG与CD相交于点P,则点P一定为△DFG的( )| A. | 外心 | B. | 内心 | C. | 垂心 | D. | 以上答案都不对 |
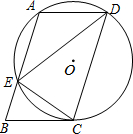 如图,在?ABCD中,过A、C、D三点的⊙O交AB于点E,连接DE、CE,∠CDE=∠BCE.
如图,在?ABCD中,过A、C、D三点的⊙O交AB于点E,连接DE、CE,∠CDE=∠BCE.