题目内容
11. 如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上,且A(-3,0),B(2,b),则正方形ABCD的面积是( )
如图,在平面直角坐标系xOy中,正方形ABCD的顶点D在y轴上,且A(-3,0),B(2,b),则正方形ABCD的面积是( )| A. | 13 | B. | 20 | C. | 25 | D. | 34 |
分析 作BM⊥x轴于M.只要证明△DAO≌△ABM,推出OA=BM,AM=OD,由A(-3,0),B(2,b),推出OA=3,OM=2,推出OD=AM=5,再利用勾股定理求出AD即可解决问题.
解答 解:作BM⊥x轴于M.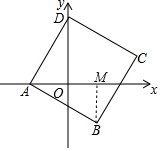
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=90°,
∴∠DAO+∠BAM=90°,∠BAM+∠ABM=90°,
∴∠DAO=∠ABM,
∵∠AOD=∠AMB=90°,
∴△DAO≌△ABM,
∴OA=BM,AM=OD,
∵A(-3,0),B(2,b),
∴OA=3,OM=2,
∴OD=AM=5,
∴AD=$\sqrt{O{A}^{2}+O{D}^{2}}$=$\sqrt{{3}^{2}+{5}^{2}}$=$\sqrt{34}$,
∴正方形ABCD的面积=34,
故选D.
点评 本题考查正方形的性质、坐标与图形的性质、全等三角形的判定和性质、勾股定理等知识,解题的关键是学会添加常用辅助线构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
1.下列三条线段,能组成三角形的是( )
| A. | 3,2,6 | B. | 3,3,6 | C. | 3,2,5 | D. | 3,3,3 |
3.下列计算正确的是( )
| A. | a+2b=3ab | B. | 3a2-2a2=1 | C. | a6÷a2=a4 | D. | a2•a4=a8 |
20.某校举行书法比赛,为奖励优胜学生,购买了一些钢笔和毛笔,钢笔单价是毛笔单价的1.6倍,购买钢笔用了1200元,购买毛笔用1500元,购买的钢笔支数比毛笔少20支,钢笔、毛笔的单价分别是多少元?如果设毛笔的单价为x元/支,那么下面所列方程正确的是( )
| A. | $\frac{1200}{1.6x}$-$\frac{1500}{x}$=20 | B. | $\frac{1500}{x}$-$\frac{1200}{1.6x}$=20 | ||
| C. | $\frac{1500}{x}$=$\frac{1200}{1.6x}$-20 | D. | $\frac{1200}{x}$-$\frac{1500}{1.6x}$=20 |
1.设a>b,则下列各式中不能成立的是( )
| A. | a+3>b+3 | B. | a-4>b-4 | C. | 2a>2b | D. | -$\frac{a}{2}$>-$\frac{b}{2}$ |