题目内容
9.在Rt△ABC中,∠C=90°,两直角边a,b分别是方程x2-7x+12=0的两个根,则AB边上的中线长为$\frac{5}{2}$.分析 先解方程求出方程的解,再根据勾股定理求出斜边,即可得出答案.
解答 解:x2-7x+12=0,
(x-3)(x-4)=0,
x-3=0,x-4=0,
x1=3,x2=4,
即直角三角形的两直角边为3,和4,
由勾股定理得:斜边AB为5,
所以AB边上的中线长为$\frac{5}{2}$.
故答案为:$\frac{5}{2}$.
点评 本题考查了勾股定理,解一元二次方程,直角三角形斜边上中线性质的应用,能求出斜边长是解此题的关键,注意:直角三角形斜边上的中线等于斜边的一半.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.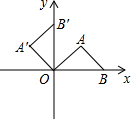 将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )
将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )
 将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )
将等腰直角三角形AOB按如图所示放置,然后绕点O逆时针旋转90°至△A′OB′的位置,点B的横坐标为2,则点A′的坐标为( )| A. | (1,1) | B. | (-1,1) | C. | (1,-1) | D. | $(-\sqrt{2},\sqrt{2})$ |
1.以下列各组数作为三角形的边长,能构成直角三角形的是( )
| A. | 4,5,6 | B. | 6,8,11 | C. | 1,1,$\sqrt{2}$ | D. | 5,12,23 |
18.已知x,y为实数,且|4x-y-2|+(2x+y-10)2=0,则( )
| A. | $\left\{\begin{array}{l}{x=2}\\{y=6}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=-2}\\{y=-6}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=-6}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-2}\\{y=6}\end{array}\right.$ |
19.已知二次函数y=$\frac{1}{4}$(x-h)2+4,当x>-1时,y随x的增大而增大,则有( )
| A. | h≥-1 | B. | h>-1 | C. | h<-1 | D. | h≤-1 |
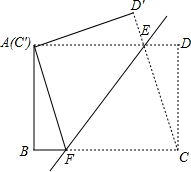 如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接AF、CE,
如图,将矩形ABCD沿直线EF折叠,使点C与点A重合,折痕交AD于点E,交BC于点F,连接AF、CE,