题目内容
2．
如图，四边形ABCD是⊙O的内接四边形，若∠DAB=60°，则∠BCD的度数是（ ）| A． | 60° | B． | 90° | C． | 100° | D． | 120° |
分析 根据圆内接四边形的性质：圆内接四边形的对角互补，求解．
解答 解：∵四边形ABCD是⊙O的内接四边形，
∴∠DAB+∠DCB=180°．
∵∠DAB=60°，
∴∠BCD=180°-60°=120°．
故选D．
点评 本题考查了圆内接四边形的性质：解答本题的关键是掌握圆内接四边形的对角互补的性质．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
12．三角形三条中线的交点叫做三角形的（ ）
| A． | 内心 | B． | 外心 | C． | 中心 | D． | 重心 |
如图，线段AB，CD表示甲、乙两幢居民楼的高，两楼间的距离BD是60米．某人站在A处测得C点的俯角为37°，D点的俯角为48°（人的身高忽略不计），求乙楼的高度CD．（参考数据：sin37°≈$\frac{3}{5}$，tan37°≈$\frac{3}{4}$，sin48°≈$\frac{7}{10}$，tan48°≈$\frac{11}{10}$）
14．计算$\sqrt{3}$×$\sqrt{5}$的结果是（ ）
| A． | $\sqrt{8}$ | B． | $\sqrt{15}$ | C． | 3$\sqrt{5}$ | D． | 5$\sqrt{3}$ |
11．-2的相反数是（ ）
| A． | -2 | B． | 2 | C． | -$\frac{1}{2}$ | D． | $\frac{1}{2}$ |
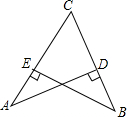如图，从小丽家C到学校A和菜市场B的夹角∠ACB是锐角，又知道从小丽家到学校A和到菜市场B的距离相等，小丽说学校A到路BC的距离AD与菜市场B到路AC的距离BE相等，你认为她说得有道理吗？请说明理由．