题目内容
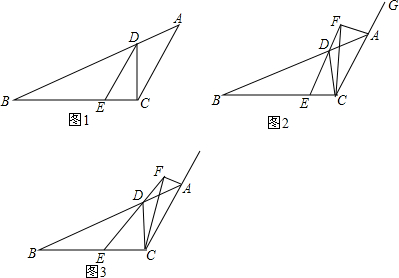
4.已知点D在△ABC的AB边上,∠ACD=∠DAC,点E在边BC上一动点.(1)如图1,若DE平分∠BDC,求证:DE∥AC;
(2)延长CA到G,点F在ED的延长线上;
①如图2,若∠DCF=$\frac{1}{3}$∠DCA,∠FAD=$\frac{1}{3}$∠BAGM∠ADC=120°,求∠AFC的度数;
②如图3,若∠EAD=$\frac{1}{3}$∠BAG,∠BDE=$\frac{1}{3}$∠BDC,猜想∠DFA与∠DAC满足的等量关系,并说明理由.
分析 (1)由三角形外角的性质得出∠BDC=∠ACD+∠DAC=2∠DAC,角平分线的性质得出∠BDE=∠BAC,得出结论;
(2)①②类比(1)的方法利用三角形外角的性质和三角形的内角和得出答案即可.
解答 解:(1)∵∠ACD=∠DAC且∠BDC=∠ACD+∠DAC,
∴∠BDC=2∠DAC,
∵DE平分∠BDC,
∴∠BDE=∠BAC,
∴DE∥AC.
(2)∵∠BAG=∠ADC+∠ACD,
∴$\frac{1}{3}$∠BAG=$\frac{1}{3}$∠ADC+$\frac{1}{3}$∠ACD,
∴∠FAG=∠FCA+$\frac{2}{3}$∠ADC且∠FAG=∠FCA+∠AFC,
∴∠AFC=80°.
(3)设∠DAC=X=∠DCA,
∴∠BDC=2X,∠BAG=180°-X,
∴∠BDE=∠FDA=$\frac{2X}{3}$,∠DAF=60°-$\frac{X}{3}$,
∴∠DFA=120°-$\frac{X}{3}$,
∴∠DFA+$\frac{1}{3}$∠DAC=120°
点评 此题考查三角形的内角和定理,外角的性质,以及角平分线的性质,综合利用基础知识解决问题.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案
相关题目
13.下列说法正确的是( )
| A. | 定理不一定是真命题 | B. | 真命题不一定正确 | ||
| C. | 假命题不一定错误 | D. | 基本事实一定是真命题 |
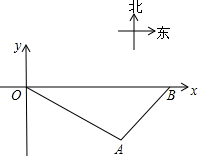 一艘轮船从O处出发,以30海里/时的速度沿东偏南30°的航线航行,两小时后到达A处.此时接到大风警报,轮船必须在1.5小时内赶到B处避风.B在O的正东方,从A处测得B的方位是北偏东45°.图所示的坐标系的单位长是1海里.
一艘轮船从O处出发,以30海里/时的速度沿东偏南30°的航线航行,两小时后到达A处.此时接到大风警报,轮船必须在1.5小时内赶到B处避风.B在O的正东方,从A处测得B的方位是北偏东45°.图所示的坐标系的单位长是1海里.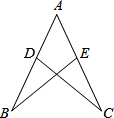 如图,已知AD=AE,BD=CE,求证:△ABE≌△ACD.
如图,已知AD=AE,BD=CE,求证:△ABE≌△ACD.