题目内容
14．已知方程x2+2x-1=0的两根是x1，x2，那么x${\;}_{1}^{2}$x2+x1x${\;}_{2}^{2}$+1=（ ）| A． | -7 | B． | 3 | C． | 7 | D． | -3 |
分析 根据根与系数的关系得到x1+x2=-2，x1x2=-1，利用因式分解的方法得到x${\;}_{1}^{2}$x2+x1x${\;}_{2}^{2}$+1=x1x2（x1+x2）+1，然后利用整体代入的方法计算．
解答 解：根据题意得x1+x2=-2，x1x2=-1，
所以x${\;}_{1}^{2}$x2+x1x${\;}_{2}^{2}$+1=x1x2（x1+x2）+1=-1×（-2）+1=3．
故选B．
点评 本题考查了根与系数的关系：若：x1，x2是一元二次方程ax2+bx+c=0（a≠0）的两根时：x1+x2=-$\frac{b}{a}$，x1x2=$\frac{c}{a}$．
练习册系列答案
阅读快车系列答案
相关题目
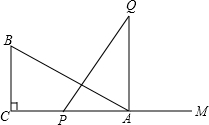如图，有一直角三角形ABC，∠C=90°，AC=10cm，BC=5cm，一条线段PQ=AB，P、Q两点分别在AC上和过A点且垂直于AC的射线AQ上运动，当P点运动到AC上什么位置时△ABC才能和以A、P、Q为顶点的三角形全等．
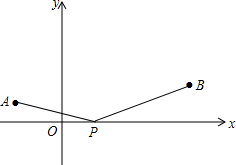如图，点A、B的坐标分别为（-1，1），（3，2），P为x轴上一点，求当BP-AP最大时和当BP+AP最小时，求P点的坐标．