题目内容
9. 如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.
如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,∠ACD=∠B.(1)求证:BC=DE;
(2)若∠A=50°,求∠BCD的度数.
分析 (1)根据AC∥DE,证得∠ACD=∠D,∠BCA=∠E,通过等量代换可知∠B=∠D,再根据AC=CE,可证△ABC≌△CDE,所以BC=DE;
(2)利用△ABC≌△CDE,得出∠A=∠DCE=50°,再利用平角的定义得出结论即可.
解答 (1)证明:∵AC∥DE,
∴∠ACD=∠D,∠BCA=∠E,
又∵∠ACD=∠B,
∴∠B=∠D,
在△ABC和△CDE中,
$\left\{\begin{array}{l}{∠B=∠D}\\{∠BCA=∠E}\\{AC=CE}\end{array}\right.$,
∴△ABC≌△CDE(AAS),
∴BC=DE.
(2)∵△ABC≌△CDE,
∴∠A=∠DCE=50°,
∴∠BCD=180°-50°=130°.
点评 本题考查三角形全等的判定方法,掌握判定两个三角形全等的一般方法:SSS、SAS、ASA、AAS、HL是解决问题的关键.

练习册系列答案
相关题目
19.若一个数的绝对值的相反数是-5,则这个数是( )
| A. | 5 | B. | -5 | C. | ±5 | D. | 0或5 |
20.方程x2=5x的根是( )
| A. | x=5 | B. | x=0 | C. | x1=0,x2=5 | D. | x1=-5,x2=0 |
1.若A=x3-2xy2+1,B=x3+xy2-3x2y,则多项式2x3-7xy2+3x2y+3的值为( )
| A. | A+B | B. | A-B | C. | 3A-B | D. | 3B-A |
19.7-4$\sqrt{3}$的算术平方根为( )
| A. | $2+\sqrt{3}$ | B. | $2-\sqrt{3}$ | C. | $\sqrt{3}-2$ | D. | $\sqrt{3}+2$ |

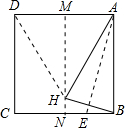 同学们,如果通过折纸能析出一个等边三角形,你相信吗?如图,先将正方形纸片对折,折痕为MN,再把B点折叠在折痕MN上,折痕为AE,点B在MN上的对应点为H,沿AH和DH剪下,则△ADH为等边三角形,请你动手试试看,并说明理由.
同学们,如果通过折纸能析出一个等边三角形,你相信吗?如图,先将正方形纸片对折,折痕为MN,再把B点折叠在折痕MN上,折痕为AE,点B在MN上的对应点为H,沿AH和DH剪下,则△ADH为等边三角形,请你动手试试看,并说明理由.