��Ŀ����
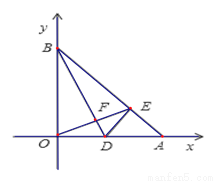
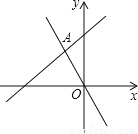
��ͼ��ֱ��AB��x���������ڵ�A��a��0������y���������ڵ�B��0��b������a��b����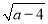 +|4-b|=0��
+|4-b|=0��
��1����A��B��������ꣻ
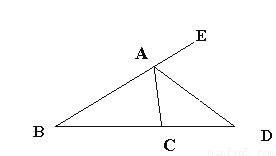
��2��DΪOA���е㣬����BD������O��OE��BD��F����AB��E����֤:��BDO=��EDA��
��3����ͼ��PΪx����A���Ҳ�����һ�㣬��BPΪ��������Rt��PBM������PB=PM��ֱ��MA��y���ڵ�Q������P��x�����˶�ʱ���߶�OQ�ij��Ƿ����仯�������䣬����ֵ�����仯�����߶�OQ��ȡֵ��Χ��
��ϰ��ϵ�д�
 ��ս100��Ԫ����Ծ�ϵ�д�
��ս100��Ԫ����Ծ�ϵ�д�
�����Ŀ


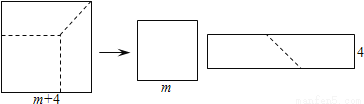
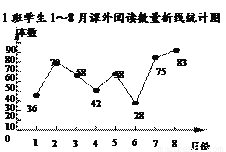
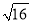 ������ƽ������ ________ ��
������ƽ������ ________ ��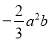 �ģ� ��
�ģ� ��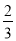 ��������2�� B. ϵ����
��������2�� B. ϵ����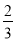 ��������3��
��������3��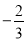 ��������2�� D. ϵ����
��������2�� D. ϵ����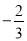 ��������3��
��������3��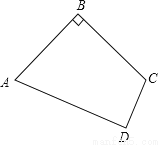
 ����λ���ȣ����2015��ʱ����P�������ǣ� ��
����λ���ȣ����2015��ʱ����P�������ǣ� ��