题目内容
3. 如图,三个全等的等腰三角形拼在一起,AB=AC=CD=DE,点B、C、E在同一条直线上,点S是DE的中点,连结BS,分别交AC、CD于点P、Q.
如图,三个全等的等腰三角形拼在一起,AB=AC=CD=DE,点B、C、E在同一条直线上,点S是DE的中点,连结BS,分别交AC、CD于点P、Q.(1)直接写出图中的两对相似三角形(相似比为1的除外);
(2)求BP:PQ:QS的值.
分析 (1)根据全等三角形的性质得到∠BAC=∠ACD=∠CDE,由平行线的判定定理得到AB∥CD∥DE,于是得到结论;
(2)根据全等三角形的性质得到∠ACB=∠DEC,由平行线的判定得到AC∥DE,推出△BPC∽△BSE,△PCQ∽△SDQ,根据相似三角形的性质得到$\frac{PB}{PS}=\frac{PC}{SE}=\frac{BC}{BE}=\frac{1}{2}$,$\frac{PC}{DS}=\frac{PQ}{QS}$,$\frac{PQ}{QS}=\frac{1}{2}$即可得到结论.
解答 解:(1)∵△ABC≌△ACD≌△DCE,
∴∠BAC=∠ACD=∠CDE,
∴AB∥CD∥DE,
∴△ABP∽△CPQ,△BPC∽△BSE;
(2)∵△ABC≌△DCE,
∴∠ACB=∠DEC,
∴AC∥DE,
∴△BPC∽△BSE,△PCQ∽△SDQ,
∴$\frac{PB}{PS}=\frac{PC}{SE}=\frac{BC}{BE}=\frac{1}{2}$,$\frac{PC}{DS}=\frac{PQ}{QS}$,
∵点S是DE的中点,
∴$\frac{PQ}{QS}=\frac{1}{2}$,
∴BP:PQ:QS=3:1:2.
点评 此题考查了相似三角形的判定和性质,全等三角形的性质,线段中点的定义,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
13.下列方程中,两个实数根之和等于2的是( )
| A. | x2-2x+3=0 | B. | x2+2x-3=0 | C. | 2x2-4x-1=0 | D. | x2-x-2=0 |
18.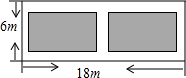 如图,某小区有一块长为18米、宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地(图中阴影部分),它们的面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道.若设人行通道的宽度为x米,则下列所列方程正确的是( )
如图,某小区有一块长为18米、宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地(图中阴影部分),它们的面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道.若设人行通道的宽度为x米,则下列所列方程正确的是( )
 如图,某小区有一块长为18米、宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地(图中阴影部分),它们的面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道.若设人行通道的宽度为x米,则下列所列方程正确的是( )
如图,某小区有一块长为18米、宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地(图中阴影部分),它们的面积之和为60平方米,两块绿地之间及周边留有宽度相等的人行通道.若设人行通道的宽度为x米,则下列所列方程正确的是( )| A. | (18-2x)(6-2x)=60 | B. | (18-3x)(6-x)=60 | C. | (18-2x)(6-x)=60 | D. | (18-3x)(6-2x)=60 |
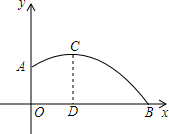 如图所示,一男生推铅球,铅球在点A处出手,出手时铅球离地面$\frac{5}{3}$m.铅球落地点在B处,铅球运行中在该男生前4m处(即0D=4)达到最高点,此时铅球离地面3m.根据图示的直角坐标系,你能算出该男生推铅球的成绩吗?
如图所示,一男生推铅球,铅球在点A处出手,出手时铅球离地面$\frac{5}{3}$m.铅球落地点在B处,铅球运行中在该男生前4m处(即0D=4)达到最高点,此时铅球离地面3m.根据图示的直角坐标系,你能算出该男生推铅球的成绩吗? 一个长方体的三视图如图所示.若其俯视图为正方形,求这个长方体的表面积.
一个长方体的三视图如图所示.若其俯视图为正方形,求这个长方体的表面积.