Question

【题目】在平面直角坐标系中，为坐标原点，点，点.

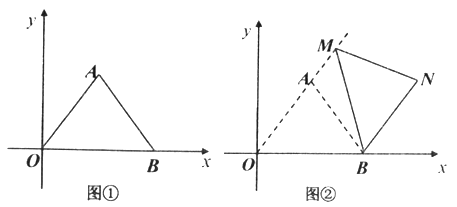
（Ⅰ）如图①，求AB的长；

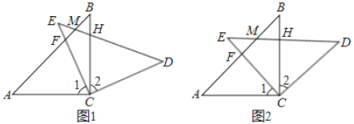
（Ⅱ）如图②，把图①中的绕点B顺时针旋转，使点O的对应点AM恰好落在OA延长线上，N是点A旋转后的对应点.

①求证：；②求点N的坐标；

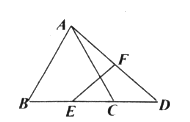
（Ⅲ）点C是OB的中点，点D为线段OA上的动点，在绕点B顺时针旋转过程中，点D的对应点是P，求线段CP长的取值范围（直接写出结果）.

Answer 1

【答案】（Ⅰ）；（Ⅱ）①见解析，②；（Ⅲ）.

【解析】

（Ⅰ）过A作，垂足为C，根据点，点得出AC和BC的长，再根据勾股得出AB的长

（Ⅱ）①根据旋转的性质可得，再根据等腰三角形的性质可得，从而得出，继而得出结论

②过N作轴，垂足为E.连接AN，根据旋转的性质和一组对边平行且相等的四边形是平行四边形得出四边形AOBN是平行四边形，得出，再根据勾股定理求出BE，从而求出点N的坐标；

（Ⅲ）过B作CP⊥AO于P，以B为圆心BP为半径画圆交BC于P1，和以B为圆心BO为半径画圆交OB的延长线于P2，得出CP的最大和最小值解答即可；

解：（Ⅰ）过A作，垂足为C，

，

.

在中，

（Ⅱ）①由（I）得

由旋转得

②过N作轴，垂足为E.连接AN

，

∴四边形AOBN是平行四边形。

在中，.

（III）如图，过B作CP⊥AO于P，以B为圆心BP为半径画圆交BC于P1， CP1有最小值，

此时

∴BP=，∴BP1=，
∴CP1的最小值为 -3=；

以B为圆心BO为半径画圆交OB的延长线于P2，，CP 2有最大值；
此时CP2=BC +BP2=3+6=9．

线段CP长的取值范围: .