题目内容
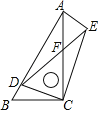
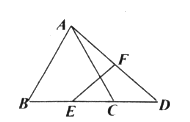
【题目】如图,在等边![]() 中,D是BC延长线上一点,
中,D是BC延长线上一点,![]() ,E,F分别是BC,AD的中点,若
,E,F分别是BC,AD的中点,若![]() ,则线段EF的长是____.
,则线段EF的长是____.
【答案】![]()
【解析】
取AB的中点M,连接EM和FM,过点E作EN⊥MF于F,根据三角形的中位线定理得出ME=1,MF=![]() ,在
,在![]() 中再根据锐角三角函数得出NE的长,继而根据勾股定理求出EF即可.
中再根据锐角三角函数得出NE的长,继而根据勾股定理求出EF即可.
取AB的中点M,连接EM和FM,过点E作EN⊥MF于F,

∵![]() 是等边三角形,
是等边三角形,
∴AB=BC=AC=2,∠ACB=60°,
∵E是BC的中点,
∴ME=![]() ,ME//AC,
,ME//AC,
∴∠ACB=∠BEM= 60°
∵F是AD的中点,
∴MF=![]() ,MF//BD,
,MF//BD,
∴∠EMF=∠BEM= 60°
在Rt![]() 中,EN=MEsin60°=
中,EN=MEsin60°=![]() ,MN= MEcos60°=
,MN= MEcos60°=![]() ,
,
∴NF=MF-MN=1
在Rt![]() 中,EF=
中,EF=![]() =
=![]()
故答案为:![]() .
.

练习册系列答案
相关题目