题目内容
【题目】已知二次函数y=﹣x2+bx+c+1。
(1)当b=1时,求这个二次函数的对称轴的方程;
(2)若c=﹣![]() b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
b2﹣2b,问:b为何值时,二次函数的图象与x轴相切?
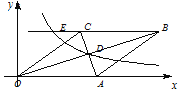
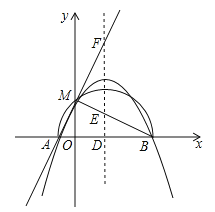
(3)若二次函数的图象与x轴交于点A(x1,0),B(x2,0),且x1<x2,b>0,与y轴的正半轴交于点M,以AB为直径的半圆恰好过点M,二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足![]() =
=![]() ,求二次函数的表达式.
,求二次函数的表达式.
【答案】(1)对称轴的方程为x=![]() ;(2)b=
;(2)b=![]() ;(3)y=﹣x2+
;(3)y=﹣x2+![]() x+1.
x+1.
【解析】试题分析:(1)二次函数y=﹣x2+bx+c+1的对称轴为x=![]() ,即可得出答案;
,即可得出答案;
(2)二次函数y=﹣x2+bx+c+1的顶点坐标为(![]() ),y由二次函数的图象与x轴相切且c=
),y由二次函数的图象与x轴相切且c=![]() b2﹣2b,得出方程组
b2﹣2b,得出方程组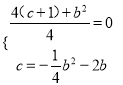 ,求出b即可;
,求出b即可;
(3)由圆周角定理得出∠AMB=90°,证出∠OMA=∠OBM,得出△OAM∽△OMB,得出OM2=OAOB,由二次函数的图象与x轴的交点和根与系数关系得出OA=﹣x1,OB=x2,x1+x2=b,x1x2=﹣(c+1),得出方程(c+1)2=c+1,得出c=0,OM=1,证明△BDE∽△BOM,△AOM∽△ADF,得出![]() ,得出OB=4OA,即x2=﹣4x1,由x1x2=﹣(c+1)=﹣1,得出方程组
,得出OB=4OA,即x2=﹣4x1,由x1x2=﹣(c+1)=﹣1,得出方程组![]() ,解方程组求出b的值即可.
,解方程组求出b的值即可.
试题解析:解:(1)二次函数y=﹣x2+bx+c+1的对称轴为x=![]() ,当b=1时,
,当b=1时, ![]() =
=![]() ,∴当b=1时,这个二次函数的对称轴的方程为x=
,∴当b=1时,这个二次函数的对称轴的方程为x=![]() .
.
(2)二次函数y=﹣x2+bx+c+1的顶点坐标为(![]() ).∵二次函数的图象与x轴相切且c=﹣
).∵二次函数的图象与x轴相切且c=﹣![]() b2﹣2b,∴
b2﹣2b,∴ ,解得:b=
,解得:b=![]() ,∴b为
,∴b为![]() ,二次函数的图象与x轴相切.
,二次函数的图象与x轴相切.
(3)∵AB是半圆的直径,∴∠AMB=90°,∴∠OAM+∠OBM=90°.∵∠AOM=∠MOB=90°,∴∠OAM+∠OMA=90°,∴∠OMA=∠OBM,∴△OAM∽△OMB,∴![]() ,∴OM2=OAOB.∵二次函数的图象与x轴交于点A(x1,0),B(x2,0),∴OA=﹣x1,OB=x2,x1+x2=b,x1x2=﹣(c+1).∵OM=c+1,∴(c+1)2=c+1,解得:c=0或c=﹣1(舍去),∴c=0,OM=1.∵二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足
,∴OM2=OAOB.∵二次函数的图象与x轴交于点A(x1,0),B(x2,0),∴OA=﹣x1,OB=x2,x1+x2=b,x1x2=﹣(c+1).∵OM=c+1,∴(c+1)2=c+1,解得:c=0或c=﹣1(舍去),∴c=0,OM=1.∵二次函数的对称轴l与x轴、直线BM、直线AM分别交于点D、E、F,且满足![]() =
=![]() ,∴AD=BD,DF=4DE,DF∥OM,∴△BDE∽△BOM,△AOM∽△ADF,∴
,∴AD=BD,DF=4DE,DF∥OM,∴△BDE∽△BOM,△AOM∽△ADF,∴![]() ,∴DE=
,∴DE=![]() ,DF=
,DF=![]() ,∴
,∴![]() ×4,∴OB=4OA,即x2=﹣4x1.∵x1x2=﹣(c+1)=﹣1,∴
×4,∴OB=4OA,即x2=﹣4x1.∵x1x2=﹣(c+1)=﹣1,∴![]() ,解得:
,解得: 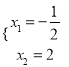 ,∴b=﹣
,∴b=﹣![]() +2=
+2=![]() ,∴二次函数的表达式为y=﹣x2+
,∴二次函数的表达式为y=﹣x2+![]() x+1.
x+1.

 名校课堂系列答案
名校课堂系列答案【题目】从2开始,连续的偶数相加,它们和的情况如下表:
加数的个数 | 连续偶数的和 |
1 |
|
2 |
|
3 |
|
4 |
|
5 |
|
(1)如果![]() 时,那么
时,那么![]() 的值为______;
的值为______;
(2)根据表中的规律猜想:用含有![]() 的代数式表示
的代数式表示![]() 的公式为:
的公式为:![]() ______;
______;
(3)根据上题的规律计算![]() 的值(要有计算过程).
的值(要有计算过程).