题目内容
已知直线l:y=mx-m2(m>0)与抛物线y=ax2有唯一公共点A,求抛物线的解析式.
考点:二次函数的性质
专题:计算题
分析:根据两函数图象的交点问题得到ax2=mx-m2,整理得ax2-mx+m2=0,由于两函数图象有有唯一公共点,则此方程有两个相等的实数解,根据判别式的意义得到△=m2-4a•m2=0,然后求出a的值,从而得到抛物线的解析式.
解答:解:根据题意得ax2=mx-m2,
整理得ax2-mx+m2=0,
因为直线l:y=mx-m2(m>0)与抛物线y=ax2有唯一公共点A,
所以△=m2-4a•m2=0,解得a=
,
所以抛物线的解析式为y=
x2.
整理得ax2-mx+m2=0,
因为直线l:y=mx-m2(m>0)与抛物线y=ax2有唯一公共点A,
所以△=m2-4a•m2=0,解得a=
| 1 |
| 4 |
所以抛物线的解析式为y=
| 1 |
| 4 |
点评:本题考查了二次函数的性质:y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-b2a,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
时,y随x的增大而增大;x>-
时,y随x的增大而减小;x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
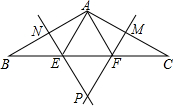 如图,已知△ABC中,∠BAC=120°,分别作AC、AB边的垂直平分线PM、PN交于点P,分别交BC于点E和点F.则以下各说法中:
如图,已知△ABC中,∠BAC=120°,分别作AC、AB边的垂直平分线PM、PN交于点P,分别交BC于点E和点F.则以下各说法中: