题目内容
6. 如图,四边形ABCD是菱形,AC=8,BD=6,DH⊥AB于H.
如图,四边形ABCD是菱形,AC=8,BD=6,DH⊥AB于H.求(1)菱形ABCD的周长;
(2)求DH的长.
分析 (1)先依据菱形的性质求得AO、OB的长,然后依据勾股定理求得AB的长,最后依据菱形ABCD的周长=4AB求解即可;
(2)由S菱形ABCD=$\frac{1}{2}$AC•BD=AB•DH,可得到DH=$\frac{AC•BD}{2AB}$,最后将AC、BD、AB的值代入计算即可.
解答 解:(1)∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC=$\frac{1}{2}$AC=4,OB=OD=$\frac{1}{2}$BD=3,
∴在Rt△ABO中,由勾股定理可知AB=5.
∴菱形ABCD的周长=5×4=20.
(2)∵S菱形ABCD=$\frac{1}{2}$AC•BD=AB•DH,
∴DH=$\frac{AC•BD}{2AB}$=4.8.
点评 本题主要考查的是菱形的性质,掌握菱形的面积公式是解题的关键.

练习册系列答案
相关题目
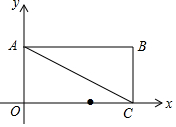 如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=1,OC=2,点D在边OC上且OD=1.25.
如图,在平面直角坐标系中,矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上,OA=1,OC=2,点D在边OC上且OD=1.25.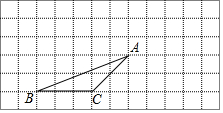 画图并填空:如图,△ABC的顶点都在每个边长为1个单位长度的方格纸的格点上,将△ABC向右平移3格,再向上平移2格.
画图并填空:如图,△ABC的顶点都在每个边长为1个单位长度的方格纸的格点上,将△ABC向右平移3格,再向上平移2格.