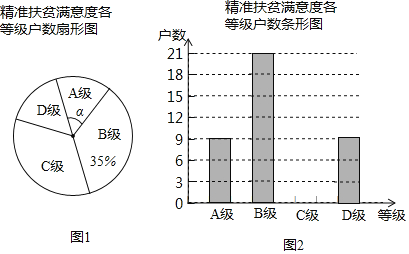
题目内容
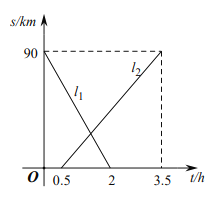
【题目】如图,在平面直角坐标系中,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,且与反比例函数
,且与反比例函数![]() 在第一象限的图象交于点
在第一象限的图象交于点![]() ,
,![]() 轴于点
轴于点![]() ,
,![]() .
.
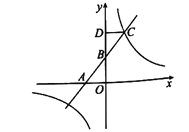
(1)求点![]() 的坐标;
的坐标;
(2)动点![]() 在
在![]() 轴上,
轴上,![]() 轴交反比例函数
轴交反比例函数![]() 的图象于点
的图象于点![]() .若
.若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]()
【解析】
(1)根据反比例函数表达式求出点C坐标,再利用“待定系数法”求出一次函数表达式,从而求出坐标;
(2)根据“P在![]() 轴上,
轴上,![]() 轴交反比例函数
轴交反比例函数![]() 的图象于点
的图象于点![]() ”及k的几何意义可求出△POQ的面积,从而求得△PAC的面积,利用面积求出点P坐标即可.
”及k的几何意义可求出△POQ的面积,从而求得△PAC的面积,利用面积求出点P坐标即可.
解:(1)∵![]() 轴于点
轴于点![]() ,
,![]() ,
,
∴点C的横坐标为2,
把![]() 代入反比例函数
代入反比例函数![]() ,得
,得![]() ,
,
∴![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() ,
,![]() 代入,得
代入,得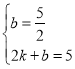 ,解得
,解得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
令![]() ,解得
,解得![]() ,
,
∴![]() ;
;
(2)∵![]() 轴,点
轴,点![]() 在反比例函数
在反比例函数![]() 的图象上,
的图象上,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
由(1)知![]() ,
,
∴![]() 或
或![]() .
.

练习册系列答案
相关题目
【题目】由于雾霾天气趋于严重,我市某电器商城根据民众健康需求,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)完成下列表格,并直接写出月销售量y(台)与售价x(元/台)之间的函数关系式及售价x的取值范围;
售价(元/台) | 月销售量(台) |
400 | 200 |
250 | |
x |
(2)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?