题目内容
【题目】![]() 两地相距
两地相距![]() ,甲、乙两人从两地出发相向而行,甲先出发.图中
,甲、乙两人从两地出发相向而行,甲先出发.图中![]() 表示两人离
表示两人离![]() 地的距离
地的距离![]() 与时间
与时间![]() 的关系,结合图象,下列结论错误的是( )
的关系,结合图象,下列结论错误的是( )
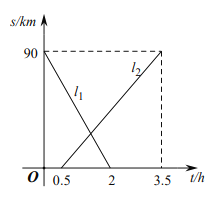
A.![]() 是表示甲离
是表示甲离![]() 地的距离与时间关系的图象
地的距离与时间关系的图象
B.乙的速度是![]()
C.两人相遇时间在![]()
D.当甲到达终点时乙距离终点还有![]()
【答案】C
【解析】
根据图像获取所需信息,再结合行程问题量间的关系进行解答即可.
解:A. ![]() 是表示甲离
是表示甲离![]() 地的距离与时间关系的图象是正确的;
地的距离与时间关系的图象是正确的;
B. 乙用时3小时,乙的速度,90÷3=![]() ,故选项B正确;
,故选项B正确;
C.设甲对应的函数解析式为y=ax+b,
则有:![]() 解得:
解得:![]()
∴甲对应的函数解析式为y=-45x+90,
设乙对应的函数解析式为y=cx+d,
则有:![]() 解得:
解得:![]()
即乙对应的函数解析式为y=30x-15
则有:![]() 解得:x=1.4h,故C选项错误;
解得:x=1.4h,故C选项错误;
D. 当甲到达终点时乙距离终点还有90-40×1.4=45km,故选项D正确;
故答案为C.

练习册系列答案
相关题目
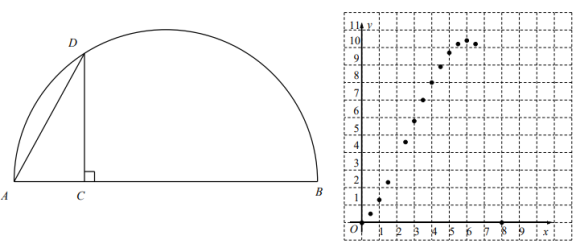
【题目】如图,![]() 是线段
是线段![]() 上--动点,以
上--动点,以![]() 为直径作半圆,过点
为直径作半圆,过点![]() 作
作![]() 交半圆于点
交半圆于点![]() ,连接
,连接![]() .已知
.已知![]() ,设
,设![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 的面积为
的面积为![]() .(当点
.(当点![]() 与点
与点![]() 或点
或点![]() 重合时,
重合时,![]() 的值为
的值为![]() )请根据学习函数的经验,对函数
)请根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行探究. (注: 本题所有数值均保留一位小数)
的变化而变化的规律进行探究. (注: 本题所有数值均保留一位小数)
![]() 通过画图、测量、计算,得到了
通过画图、测量、计算,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
补全表格中的数值: ![]() ;
;![]() ;
;![]() .
.
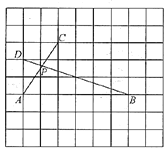
![]() 根据表中数值,继续描出
根据表中数值,继续描出![]() 中剩余的三个点
中剩余的三个点![]() ,画出该函数的图象并写出这个函数的一条性质;
,画出该函数的图象并写出这个函数的一条性质;
![]() 结合函数图象,直接写出当
结合函数图象,直接写出当![]() 的面积等于
的面积等于![]() 时,
时,![]() 的长度约为___ _
的长度约为___ _![]() .
.