Question

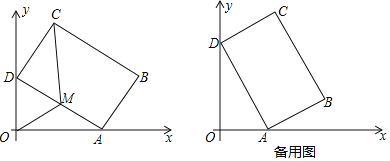
【题目】如图，在梯形中，，，，．点是线段上的动点，点、分别是线段、上的点，且，联结、．

（1）求证：；

（2）当时，如果是以为腰的等腰三角形，求线段的长；

（3）当时，求的正切值．（用含的式子表示）

Answer 1

【答案】（1）详见解析；（2）；（3）

【解析】

（1）先利用两边对应成比例，夹角相等，判断出，得出∠DQE=∠BDC，即可得出结论；
（2）先用△DEQ∽△BCD，得出比例式表示出EQ，再分两种情况，建立方程求解，即可得出结论；
（3）先判得出△PHQ∽△BGD，得出，进而表示出，，即可得出结论．

解：（1）∵，∴．

∵，，∴．

∴．

∴，∴．

（2）设的长为，则，．

∵，∴，∴．

（ⅰ）当时，

∴，

∵，∴，∴，

∴，∴，∴，

解得，或（舍去）．

（ⅱ）当时，

∴，解得，

∵，∴此种情况不存在．

∴．

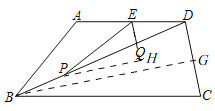
（3）过点作，交的延长线于点；过点作，垂足为点．

∵，，∴，，

∵，∴．

∵，∴．

又∵，

∴．

∴，∴．

∴，．

∴，

∴．