题目内容
19．设直角三角形的两条直角边分别为a和b，斜边长为c，已知b=12，c=13，则a=（ ）| A． | 1 | B． | 5 | C． | 10 | D． | 25 |
分析 直接根据勾股定理即可得出结论．
解答 解：∵直角三角形的两条直角边分别为a和b，斜边长为c，b=12，c=13，
∴a=$\sqrt{{c}^{2}-{b}^{2}}$=$\sqrt{{13}^{2}-{12}^{2}}$=5．
故选B．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
相关题目
11．化简$\sqrt{（m-5）^{2}（5-m）}$的正确结果是（ ）
| A． | （m-5）$\sqrt{5-m}$ | B． | （5-m）$\sqrt{5-m}$ | C． | m-5$\sqrt{-（5-m）}$ | D． | 5-m$\sqrt{5-m}$ |
11．在直线MN上取一点P，过点P作射线PA，PB，使PA⊥PB，当∠MPA=40°，则∠NPB的度数是（ ）
| A． | 50° | B． | 60° | C． | 40°或140° | D． | 50°或130° |
如图，矩形ABCD中，点E为AB中点，连接CE，将顶点B沿CE折叠至点P处，连接AP并延长交边CD于点F，
如图，直线AB、CD相交于点O，OE⊥OC，若∠1=50°，分别求∠2，3的度数．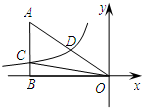
如图已知双曲线y=$\frac{k}{x}$（k＜0）经过直角△OAB斜边OA的中点D，且与直角边AB交于点C，若点A坐标为（-6，4），则△AOC的面积为（ ）