Question

八年级学生准备测量校园人工湖的深度，他们把一根竹竿垂直插到离湖边1米的水底，只见竹竿高出水面1尺，把竹竿的顶端拉向湖边（底端不变），竿顶和湖沿的水面刚好平齐，求湖水的深度和竹竿的长．

Answer 1

考点：勾股定理的应用

专题：

分析：设湖水深h尺，则竹竿高（h+1）尺，再根据勾股定理求出h的值即可．

解答：解：设湖水深h尺，则竹竿高（h+1）尺，
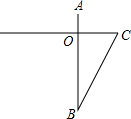
在Rt△BOC中，
∵OB=h，BC=h+1，OC=1米=3尺，
∴3²+h²=（h+1）²，
解得h=4，
∴h+1=5．
答：湖水深4尺，竹竿长5尺．

点评：本题考查的是勾股定理的应用，在应用勾股定理解决实际问题时勾股定理与方程的结合是解决实际问题常用的方法，关键是从题中抽象出勾股定理这一数学模型，画出准确的示意图．领会数形结合的思想的应用．