Question

17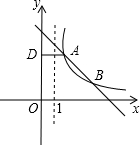．已知函数y=$\frac{m}{x-1}$（x＞1，m＞0）的图象C是由函数y=$\frac{m}{x}$（x＞0，m＞0）的图象向右平移一个单位得到，如图所示，函数y=-x+5的图象与图象C交于A，B两点，作AD⊥y轴，垂足为D．
（Ⅰ）求实数m的取值范围；
（Ⅱ）若AB=$\sqrt{2}$AD，求实数m的值．

Answer 1

分析 （Ⅰ）联立方程，整理得到关于x的一元二次方程，根据题意得到△=36-4（5+m）＞0，从而求得m的取值；
（Ⅱ）设A（x₀，$\frac{m}{{x}_{0}-1}$），由AB=$\sqrt{2}$AD，得到B（2x₀，$\frac{m}{2{x}_{0}-1}$），把A、B代入y=-x+5得到方程组，解方程组求得m的值．

解答 解（Ⅰ）联立方程组$\left\{\begin{array}{l}{y=-x+5}\\{y=\frac{m}{x-1}}\end{array}\right.$，
整理得x²-6x+5+m=0，
∵函数y=-x+5的图象与图象C交于A，B两点，
∴△=36-4（5+m）＞0，
∵m＞0，
∴0＜m＜4；
（Ⅱ）设A（x₀，$\frac{m}{{x}_{0}-1}$），
∵AB=$\sqrt{2}$AD，
∴B（2x₀，$\frac{m}{2{x}_{0}-1}$），
把A、B代入y=-x+5得$\left\{\begin{array}{l}{\frac{m}{{x}_{0}-1}=-{x}_{0}+5}\\{\frac{m}{2{x}_{0}-1}=-2{x}_{0}+5}\end{array}\right.$，
解得m=3．

点评 本题考查了反比例函数和一次函数的交点问题，根据题意列出方程组是解题的关键．