题目内容
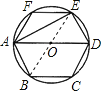
【题目】如图,若六边形![]() 是
是![]() 的内接正六边形,则
的内接正六边形,则![]() ________,
________,![]() ________,
________,![]() ________,
________,![]() ________.
________.

【答案】90° 30°, 60°, 120
【解析】
连接OE,OB,由六边形ABCDEF是⊙O的内接正六边形,即可求得圆心角∠EOD=∠AOB=60°,即可判定△OED与△OAB是等边三角形,根据等边三角形的性质,即可求得∠DAB与∠EDA的度数,然后根据圆周角定理,求得∠EAD的度数,由三角形的内角和定理,即可求得∠AED的度数,然后根据正六边形的性质,求得∠AFE的度数,由等腰三角形的性质,求得∠FAE的度数.
连接OE,OB,
∵六边形ABCDEF是⊙O的内接正六边形,
∴∠EOD=∠AOB=![]() ×360°=60°,
×360°=60°,
∵OE=OD,OA=OB,
∴△OED与△OAB是等边三角形,
∴∠ADE=∠DAB=60°;
∴∠EAD=![]() ∠EOD=
∠EOD=![]() ×60°=30°,
×60°=30°,
∴∠AED=180°-∠EAD-∠ADE=90°;
∵六边形ABCDEF是正六边形,
∴∠EFA=![]() =120°,
=120°,
∵AF=EF,
∴∠FAE=![]() =30°.
=30°.
∴∠AED=90°,∠FAE=30°,∠DAB=60°,∠EFA=120°.
故答案为:90°,30°,60°,120°.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案【题目】某公司根据市场计划调整投资策略,对![]() ,
,![]() 两种产品进行市场调查,收集数据如表:
两种产品进行市场调查,收集数据如表:
项目 产品 | 年固定成本 (单位:万元) | 每件成本 (单位:万元) | 每件产品销售价 (万元) | 每年最多可生产的件数 |
|
|
|
|
|
|
|
|
|
|
其中![]() 是待定常数,其值是由生产
是待定常数,其值是由生产![]() 的材料的市场价格决定的,变化范围是
的材料的市场价格决定的,变化范围是![]() ,销售
,销售![]() 产品时需缴纳
产品时需缴纳![]() 万元的关税,其中
万元的关税,其中![]() 为生产产品的件数,假定所有产品都能在当年售出,设生产
为生产产品的件数,假定所有产品都能在当年售出,设生产![]() ,
,![]() 两种产品的年利润分别为
两种产品的年利润分别为![]() 、
、![]() (万元),写出
(万元),写出![]() 、
、![]() 与
与![]() 之间的函数关系式,注明其自变量
之间的函数关系式,注明其自变量![]() 的取值范围.
的取值范围.
【题目】国家实行一系列“三农”优惠政策后,农民收入大幅度增加.某乡所辖村庄去年的年人均收入(单位:元)情况如下表:
年人均收入 | 3 500 | 3 700 | 3 800 | 3 900 | 4 500 |
村庄个数 | 1 | 1 | 3 | 3 | 1 |
该乡去年各村庄年人均收入的中位数是( )
A.3 700元B.3 800元C.3 850元D.3 900元



