Question

【题目】已知：如图，在平面直角坐标系中，点、的坐标分别为，．

求的长；

过点作，交轴于点，求点的坐标；

在的条件下，如果、分别是和上的动点，连接，设，问是否存在这样的使得与相似？若存在，请求出的值；若不存在，请说明理由．

Answer 1

【答案】的长为；的坐标为；存在，的值为或．

【解析】

（1）根据点A、B的坐标分别为A（-4，0），B（0，3）可知OB=3，AO=4，利用勾股定理即可求出AB．
（2）根据BC⊥AB，BO⊥AC，利用射影定理即可求出OC，然后可知C点的坐标．
（3）假设△APQ与∽△ABC，利用其对应边成比例即可求出x的值．

(1)∵点A.B的坐标分别为A(4,0),B(0,3)，

∴OB=3，AO=4，

∴

(2)∵BC⊥AB，BO⊥AC，

∴ 即

∴C点的坐标是(2.25,0)；

(3)

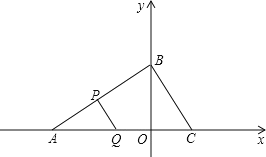
当△APQ与∽△ABC时,PQ∥BC，

∴

∵AP=CQ=x，

∴

解得

当△APQ与∽△ACB时,

即

解得：.

答：(1)AB的长为5;(2)C的坐标为(2.25,0);(3)存在,x的值为或．