题目内容
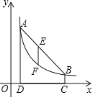
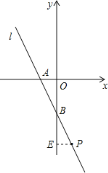
【题目】如图,已知,直线![]() 分别交
分别交![]() 轴
轴![]() 轴于
轴于![]() 、
、![]() 两点,
两点,![]() 、
、![]() 的长满足
的长满足![]() ,点
,点![]() 是直线
是直线![]() 上一点,且
上一点,且![]() .
.

![]() 求直线
求直线![]() 的解析式;
的解析式;
![]() 求过点
求过点![]() 的反比例函数解析式;
的反比例函数解析式;
![]() 点
点![]() 在反比例函数图象上是否存在一点
在反比例函数图象上是否存在一点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点,
为顶点,![]() 为腰的四边形为梯形?若存在,请直接写出点
为腰的四边形为梯形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】![]() ;
;![]() ;
;![]() 的坐标是
的坐标是![]() .
.
【解析】
(1)根据非负数的性质求得OA和OB的长,即A和B的坐标,利用待定系数法求得直线l的解析式;
(2)AP=2BP,则AB=BP,作PE⊥y轴于点E,证明△AOB≌△PEB,求得PE和OE的长,则P的坐标即可求得,然后利用待定系数法求得反比例函数解析式;
(3)点A、B、C、D为顶点,AC为腰的四边形为梯形,则是梯形ABDC,其中D在第四象限,求得CD的解析式,然后解直线CD的解析式和反比例函数解析式的交点即可求解.
![]() ∵
∵![]() ,
,
∴![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
则![]() 的坐标是
的坐标是![]() ,
,![]() 的坐标是
的坐标是![]() ,
,
设直线![]() 的解析式是
的解析式是![]() ,根据题意得:
,根据题意得:![]() ,
,
解得: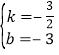 ,
,
则直线![]() 的解析式是
的解析式是![]() ;
;
![]() ∵
∵![]() ,
,
∴![]() ,
,
作![]() 轴于点
轴于点![]() .
.
在![]() 和
和![]() 中,
中,
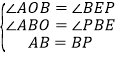 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,即
,即![]() ,
,
∴![]() 的坐标是
的坐标是![]() .
.
设反比例函数的解析式是![]() ,把
,把![]() 代入得:
代入得:![]() ,
,
则反比例函数的解析式是:![]() ;
;
![]() 点
点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点,
为顶点,![]() 为腰的四边形为梯形,
为腰的四边形为梯形,
则是梯形![]() ,其中
,其中![]() 在第四象限.
在第四象限.
设直线![]() 的解析式是
的解析式是![]() ,把
,把![]() 代入解析式得:
代入解析式得:![]() ,
,
解得:![]() ,
,
则直线![]() 的解析式是:
的解析式是:![]() .
.
解方程组 ,
,
解得:![]() 或
或![]() (舍去).
(舍去).
则![]() 的坐标是
的坐标是![]() .
.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目