Question

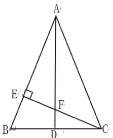
【题目】如图，将△ABC分别沿AB，AC翻折得到△ABD 和△AEC，线段BD与AE交于点 F，连接BE .

（1）如果∠ABC=16，∠ACB=30°，求∠DAE的度数；

（2）如果BD⊥CE，求∠CAB 的度数．

Answer 1

【答案】（1） ∠DAE=42°;（2）∠CAB =135°.

【解析】

（1）已知，,可由三角形的内角和求出的度数，已知△ABC分别沿AB，AC翻折得到△ABD 和△AEC，所以可得 ，,从而可求出；
（2）当时，,已知△ABC分别沿AB，AC翻折得到△ABD 和△AEC，所以可得,,所以,最后由三角形内角和求出即可.

解：（1）∵△ABC沿AC、AB翻折得到△AEC和△ABD，

∴.

∴.

.

∵，

∴.

∴.

（2）∵，

∴.

∴.

∵，

∴.

∴.