题目内容
16.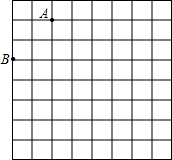 如图是8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),请在所给网格中按下列要求操作:
如图是8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),请在所给网格中按下列要求操作:(1)在网格中建立平面直角坐标系,使A点坐标为(-3,5),B点坐标为(-5,3).
(1)按(1)中的平面直角坐标系在第二象限内的格点上找点C,使点C与线段AB组成以AB为底的等腰三角形,且AC=$\sqrt{10}$,则C点坐标为(-2,2),△ABC的周长为2$\sqrt{10}$+2$\sqrt{2}$,面积是2$\sqrt{6}$.
分析 (1)由直角坐标系性质可直接作出图
(2)在线段AB的垂直平分线上,且经过格点的点为C点.由图可知该点并求出周长和面积.
解答  解:(1)依题意作出直角坐标系如图:
解:(1)依题意作出直角坐标系如图:
(2)点C在线段AB的垂直平分线上,且经过格点,
∵AC=$\sqrt{10}$,
∴当该点为(-2,2)时,三角形为等腰直角三角形,腰长AB=BC=$\sqrt{10}$,AB=2$\sqrt{2}$,
此时三角形周长为:2×$\sqrt{10}$+2$\sqrt{2}$=2$\sqrt{10}$+2$\sqrt{2}$;
面积=$\frac{1}{2}$×2$\sqrt{2}$×2$\sqrt{3}$=2$\sqrt{6}$,
故答案为:(-2,2),2$\sqrt{10}$+2$\sqrt{2}$,2$\sqrt{6}$.
点评 本题考查了等腰三角形的判定和性质,坐标与图形的性质,勾股定理,三角形的周长和面积,熟练掌握等腰三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
 如图,在Rt△ABC中,斜边BC上的高AD=4,cosB=$\frac{4}{5}$,求∠BAD的正弦值和余弦值及AC的长度.
如图,在Rt△ABC中,斜边BC上的高AD=4,cosB=$\frac{4}{5}$,求∠BAD的正弦值和余弦值及AC的长度.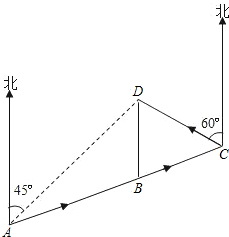 为解决郑州交通拥堵的问题,政府决定北在A、D两地修建高架路,为此,公交车不得不更改线路,原来直接由A到D的公交车现改为由A-B-C-D,如图,其中A、B、C三地在同一直线上,D地在A地北偏东45°方向,在B地正北方向,在C地北偏西60°方向.C地在A地北偏东75°方向,B、D两地相距2km.问更改线路后公交车多行了多远?(结果保留整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7)
为解决郑州交通拥堵的问题,政府决定北在A、D两地修建高架路,为此,公交车不得不更改线路,原来直接由A到D的公交车现改为由A-B-C-D,如图,其中A、B、C三地在同一直线上,D地在A地北偏东45°方向,在B地正北方向,在C地北偏西60°方向.C地在A地北偏东75°方向,B、D两地相距2km.问更改线路后公交车多行了多远?(结果保留整数,参考数据:$\sqrt{2}$≈1.4,$\sqrt{3}$≈1.7) 如图,在四边形ABCD中,E、F分别在BC、AD上,且AF=CE,连接EF,与对角线BD交于点O.若EF、BD互相平分,试判断四边形ABCD的形状,并说明理由.
如图,在四边形ABCD中,E、F分别在BC、AD上,且AF=CE,连接EF,与对角线BD交于点O.若EF、BD互相平分,试判断四边形ABCD的形状,并说明理由.