题目内容
6. 如图,在Rt△ABC中,斜边BC上的高AD=4,cosB=$\frac{4}{5}$,求∠BAD的正弦值和余弦值及AC的长度.
如图,在Rt△ABC中,斜边BC上的高AD=4,cosB=$\frac{4}{5}$,求∠BAD的正弦值和余弦值及AC的长度.
分析 由AD⊥BC,于是得到∠ADB=∠BAC=90°,根据三角形的内角和定理求出∠B=∠CAD,根据已知条件cosB=$\frac{BD}{AB}$=$\frac{4}{5}$,于是得到sin∠BAD=$\frac{BD}{AB}$=$\frac{4}{5}$,求得cos∠BAD=$\sqrt{1-si{n}^{2}∠BAD}$=$\frac{3}{5}$,根据同角的三角函数的关系得到tan∠BAD=$\frac{sin∠BAD}{cos∠BAD}$=$\frac{4}{3}$,根据cos∠CAD=$\frac{AD}{AC}$=$\frac{4}{5}$,把AD的值代入求出AC即可.
解答 解:∵AD⊥BC,
∴∠ADB=∠BAC=90°,
∴∠B=∠CAD,
∵cosB=$\frac{BD}{AB}$=$\frac{4}{5}$,
∴sin∠BAD=$\frac{BD}{AB}$=$\frac{4}{5}$,
∴cos∠BAD=$\sqrt{1-si{n}^{2}∠BAD}$=$\frac{3}{5}$,
∴tan∠BAD=$\frac{sin∠BAD}{cos∠BAD}$=$\frac{4}{3}$,
∵cos∠CAD=$\frac{AD}{AC}$=cos∠B=$\frac{4}{5}$,AD=4,
∴AC=5.
点评 本题考查了解直角三角形中三角函数的应用,熟练掌握边角之间的关系是解题的关键.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案
相关题目
16.已知命题A:“关于x的一元二次方程x2-ax+1=0一定有实根”.在下列选项中,可以作为“命题A是假命题”的反例的是( )
| A. | a=2 | B. | a=0 | C. | a=-2 | D. | a=-4 |
17.下列说法正确的是( )
| A. | 3是9的算术平方根 | B. | -3是(-3)2的算术平方根 | ||
| C. | 0.64的立方根是0.4 | D. | $\sqrt{(-2)^{2}}$的平方根是±2 |
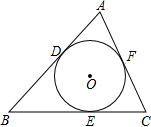 如图,⊙O是△ABC的内切圆,切点分别为D,E,F.若AB=6,BC=5,AC=4,求AD,CF.
如图,⊙O是△ABC的内切圆,切点分别为D,E,F.若AB=6,BC=5,AC=4,求AD,CF. 已知二次函数图象的顶点是(-1,2),且过点$({0,\frac{3}{2}})$.
已知二次函数图象的顶点是(-1,2),且过点$({0,\frac{3}{2}})$.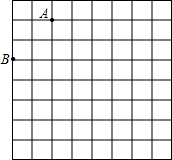 如图是8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),请在所给网格中按下列要求操作:
如图是8×8的正方形网格(小正方形的边长为1,小正方形的顶点叫格点),请在所给网格中按下列要求操作: