题目内容
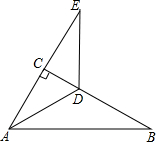如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AD平分∠CAB．（1）求∠CAD的度数；
（2）延长AC至E，使CE=AC，求证：DA=DE．
考点：全等三角形的判定与性质
专题：证明题
分析：（1）利用“直角三角形的两个锐角互余”的性质和角平分的性质进行解答；
（2）通过证△ACD≌△ECD来推知DA=DE．
（2）通过证△ACD≌△ECD来推知DA=DE．
解答：（1）解：如图，∵在Rt△ABC中，∠ACB=90°，∠B=30°，
∴∠B=30°，
∴∠CAB=60°．
又∵AD平分∠CAB，
∴∠CAD=
∠CAB=30°，即∠CAD=30°；
（2）证明：∵∠ACD+∠ECD=180°，且∠ACD=90°，
∴∠ECD=90°，
∴∠ACD=∠ECD．
在△ACD与△ECD中，
，
∴△ACD≌△ECD（SAS），
∴DA=DE．
∴∠B=30°，
∴∠CAB=60°．
又∵AD平分∠CAB，
∴∠CAD=
| 1 |
| 2 |
（2）证明：∵∠ACD+∠ECD=180°，且∠ACD=90°，
∴∠ECD=90°，
∴∠ACD=∠ECD．
在△ACD与△ECD中，
|
∴△ACD≌△ECD（SAS），
∴DA=DE．
点评：本题考查了全等三角形的判定与性质．在应用全等三角形的判定时，要注意三角形间的公共边和公共角，必要时添加适当辅助线构造三角形．
练习册系列答案
相关题目
抛物线y=-x2-6x-11的顶点坐标是（ ）
| A、（3，2） |
| B、（3，-2） |
| C、（-2，2） |
| D、（-3，-2） |
如图，AB是⊙O的直径，弦CD⊥AB于点E，点P在⊙O上，∠1=∠BCD．
如图有A、B两个大小均匀的转盘，其中A转盘被分成3等份，B转盘被分成4等份，并在每一份内标上数字．小明和小红同时各转动其中一个转盘，转盘停止后（当指针指在边界线时视为无效，重转），若将A转盘指针指向的数字记作一次函数表达式中的k，将B转盘指针指向的数字记作一次函数表达式中的b．
如图，AB是⊙O的直径，C、D两点在⊙O上，且BC=CD，过点C作CE⊥AD，交AD的延长线于点E，交AB的延长线于点F．