题目内容
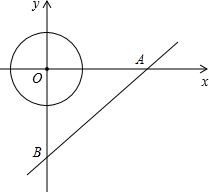 如图,在平面直角坐标系中,直线y=
如图,在平面直角坐标系中,直线y=| 3 |
| 4 |
考点:直线与圆的位置关系,一次函数图象上点的坐标特征
专题:
分析:如图,当圆心点P在点A的左侧时,连接PC;首先求出AB的长;然后证明△APC∽△ABO,得到
=
,求出PA的值,即可解决问题;当圆心点P在点A的右侧时,同理可求出OP的值,即可解决问题.
| AP |
| AB |
| PC |
| OB |
解答: 解:如图,当⊙O的圆心运动到点P处时,⊙P与直线AB相切;
解:如图,当⊙O的圆心运动到点P处时,⊙P与直线AB相切;
连接PC,则PC⊥AB;对于直线y=
x-3,
当x=0时,y=-3;当y=0时,x=4,
∴OA=4,OB=3;由勾股定理得:AB=
=5;
∵∠AOB=∠ACP=90°,∠PCA=∠BOA,
∴△APC∽△ABO,
∴
=
,
解得:PA=
,OP=4-
=
,
∴经过
秒,动圆与直线AB相切.
当圆心O运动到点A的右侧时,同理可求:
PA=
,PO=4+
=
,
∴经过
秒,动圆与直线AB相切.
综上所述,经过
或
秒,动圆与直线AB相切.
 解:如图,当⊙O的圆心运动到点P处时,⊙P与直线AB相切;
解:如图,当⊙O的圆心运动到点P处时,⊙P与直线AB相切;连接PC,则PC⊥AB;对于直线y=
| 3 |
| 4 |
当x=0时,y=-3;当y=0时,x=4,
∴OA=4,OB=3;由勾股定理得:AB=
| 32+42 |
∵∠AOB=∠ACP=90°,∠PCA=∠BOA,
∴△APC∽△ABO,
∴
| AP |
| AB |
| PC |
| OB |
解得:PA=
| 5 |
| 3 |
| 5 |
| 3 |
| 7 |
| 3 |
∴经过
| 7 |
| 3 |
当圆心O运动到点A的右侧时,同理可求:
PA=
| 4 |
| 3 |
| 4 |
| 3 |
| 16 |
| 3 |
∴经过
| 16 |
| 3 |
综上所述,经过
| 7 |
| 3 |
| 16 |
| 3 |
点评:该题主要考查了直线与圆的位置关系及其应用问题;解题的关键是作辅助线;灵活运用直线与圆的位置关系、相似三角形的判定与性质等几何知识点来分析、判断、解答.

练习册系列答案
相关题目
下列说法正确的是( )
| A、近似数4.60精确到十分位 |
| B、近似数5000万精确到个位 |
| C、近似数4.31万精确到0.01 |
| D、1.45×104精确到百位 |
 如图,在四边形ABCD中,AB=6,BC=8,∠A=120°,∠B=60°,∠BCD=150°.求AD的长.
如图,在四边形ABCD中,AB=6,BC=8,∠A=120°,∠B=60°,∠BCD=150°.求AD的长. 如图所示,AD、CE是△ABC的高,AB=10,BD=8,CD=4,AD=6,求CE的长.
如图所示,AD、CE是△ABC的高,AB=10,BD=8,CD=4,AD=6,求CE的长.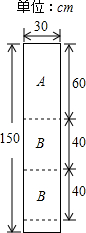 某公司装修需用A型板材240块,B型板材180块,A型板材规格是60cm×30cm,B型板材规格是40cm×30cm.现只能购得规格是150cm×30cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材,共有下列三种裁法:(如图是裁法一的裁剪示意图)
某公司装修需用A型板材240块,B型板材180块,A型板材规格是60cm×30cm,B型板材规格是40cm×30cm.现只能购得规格是150cm×30cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材,共有下列三种裁法:(如图是裁法一的裁剪示意图)