Question

如图，已知△ABC的周长是24，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于D，且OD=3，则△ABC的面积是

 

．

Answer 1

考点：角平分线的性质

专题：

分析：根据角平分线上的点到角的两边的距离相等可得点O到AB、AC、BC的距离都相等，从而可得到△ABC的面积等于周长的一半乘以OD，然后列式进行计算即可求解．

解答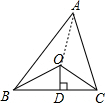：解：如图，连接OA，
∵OB、OC分别平分∠ABC和∠ACB，
∴点O到AB、AC、BC的距离都相等，
∵△ABC的周长是24，OD⊥BC于D，且OD=3，
∴S_△ABC=

1

2

×24×3=36，
故答案为：36．

点评：本题考查了角平分线上的点到角的两边的距离相等的性质，判断出三角形的面积与周长的关系是解题的关键．