题目内容
2.按要求解下列方程:(1)2x2-4x-7=0(配方法)
(2)-3t2-2t+4=0(公式法)
分析 (1)方程整理后,利用配方法求出解即可;
(2)方程利用公式法求出解即可.
解答 解:(1)方程整理得:x2-2x=$\frac{7}{2}$,
配方得:x2-2x+1=$\frac{9}{2}$,即(x-1)2=$\frac{9}{2}$,
开方得:x-1=±$\frac{3\sqrt{2}}{2}$,
解得:x1=1+$\frac{3\sqrt{2}}{2}$,x2=1-$\frac{3\sqrt{2}}{2}$;
(2)这里a=-3,b=-2,c=4,
∵△=4+48=52,
∴t=$\frac{2±\sqrt{52}}{-6}$=$\frac{-1±\sqrt{13}}{3}$.
点评 此题考查了解一元二次方程-配方法及公式法,熟练掌握各种解法是解本题的关键.

练习册系列答案
相关题目
10.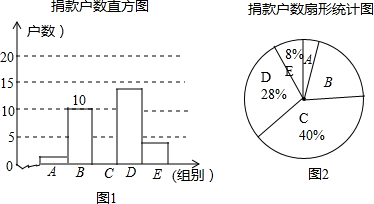 我市政府积极组织社区居民为希望工程捐款,为了解阳光社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图所示的不完整统计图.已知A、B两组捐款户数直方图的高度比为1:5,请结合图中相关数据回答下列问题
我市政府积极组织社区居民为希望工程捐款,为了解阳光社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图所示的不完整统计图.已知A、B两组捐款户数直方图的高度比为1:5,请结合图中相关数据回答下列问题
(1)A组捐款户数是多少?本次调查的样本容量是多少?
(2)求出C组的频数并补全直方图;
(3)若该社区有500户住户,请估计捐款不少于300元的户数是多少?
 我市政府积极组织社区居民为希望工程捐款,为了解阳光社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图所示的不完整统计图.已知A、B两组捐款户数直方图的高度比为1:5,请结合图中相关数据回答下列问题
我市政府积极组织社区居民为希望工程捐款,为了解阳光社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图所示的不完整统计图.已知A、B两组捐款户数直方图的高度比为1:5,请结合图中相关数据回答下列问题(1)A组捐款户数是多少?本次调查的样本容量是多少?
(2)求出C组的频数并补全直方图;
(3)若该社区有500户住户,请估计捐款不少于300元的户数是多少?
| 组别 | 捐款额(x)元 |
| A | 10≤x<100 |
| B | 100≤x<200 |
| C | 200≤x<300 |
| D | 300≤x<400 |
| E | x≥400 |
17.下列方程中,是关于x的一元二次方程的是( )
| A. | $\frac{1}{{x}^{2}}$+$\frac{1}{x}$-2=0 | B. | 2x(x+2)=(2x+1)(x-1) | C. | $\frac{2{x}^{2}+1}{3}$=$\frac{x+1}{2}$ | D. | ax2+ba+c=0 |
7.计算(-2)2012+(-2)2013的结果是( )
| A. | 22013 | B. | -22012 | C. | -22013 | D. | -2 |
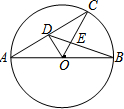 如图,AB是⊙O的直径,AC是弦.OD⊥AC于D,OC与BD交于E,若BD=6,则DE等于( )
如图,AB是⊙O的直径,AC是弦.OD⊥AC于D,OC与BD交于E,若BD=6,则DE等于( )