题目内容
19. 如图,已知Rt△ABC中,∠B=90°,且AB=2BC,请在图中按如下要求进行操作和证明:
如图,已知Rt△ABC中,∠B=90°,且AB=2BC,请在图中按如下要求进行操作和证明:(1)用圆规在CA上截取CD=CB,保留痕迹,标注点D;再以点A为圆心,AD为半径画弧交AB于点P,保留痕迹,标注点P;
(2)证明点P是线段AB的黄金分割点.
分析 (1)根据题意进行尺规作图即可;
(2)设BC=x,根据勾股定理、结合图形求出$\frac{AP}{AB}$=$\frac{\sqrt{5}-1}{2}$即可.
解答 解: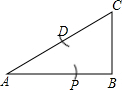 (1)如图所示:
(1)如图所示:
(2)设BC=x,则AB=2x,AC=$\sqrt{5}$x,
由题意得,CD=x,
则AP=AD=($\sqrt{5}$-1)x,
$\frac{AP}{AB}$=$\frac{\sqrt{5}-1}{2}$,
则点P是线段AB的黄金分割点.
点评 本题考查的是黄金分割的概念,把线段AB分成两条线段AC和BC(AC>BC),且使AC是AB和BC的比例中项(即ABAC=ACBC),叫做把线段AB黄金分割,点C叫做线段AB的黄金分割点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

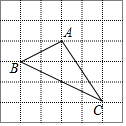 如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点A、B、C为顶点的三角形的面积是4,周长是3$\sqrt{5}$+$\sqrt{13}$.
如图,正方形网格中每个小正方形的边长都是1,每个小正方形的顶点叫做格点,以格点A、B、C为顶点的三角形的面积是4,周长是3$\sqrt{5}$+$\sqrt{13}$.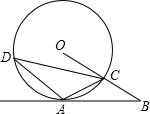 已知:如图A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,∠B=30°.
已知:如图A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,∠B=30°. 如图,已知BC∥DE,$\frac{AB}{AD}$=$\frac{3}{2}$,若BD=10cm,ED=6cm,求AD和BC的长度.
如图,已知BC∥DE,$\frac{AB}{AD}$=$\frac{3}{2}$,若BD=10cm,ED=6cm,求AD和BC的长度.