题目内容
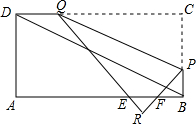
如图所示,在矩形ABCD中,E为BC中点,ED交AC于点P,DQ⊥AC于点Q,AB=kBC.
(1)当k=1时, =______;
=______;
(2)当k= 时,求证PQ=CP;
时,求证PQ=CP;
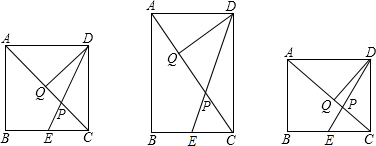
(3)当k=______时,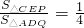 .
.
解:(1)∵在矩形ABCD中,AB=BC,
∴矩形ABCD是正方形,
∵AD∥EC,
∴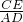 =
= ,
,
∵E为BC中点,
∴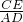 =
= =
= ,
,
∴ =
= ;
;
故答案为: ;
;
(2)∵Rt△ACD中,DQ⊥AC,
∴△ADQ∽△DCQ∽△ACD,
∴AD2=AQ•AC,CD2=CQ•AC,
∴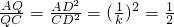
∴QC=2AQ,
又 =
= =2,∴AP=2PC,
=2,∴AP=2PC,
∴AQ=PQ=PC;
(3) .
.
∵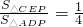 ,当
,当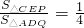 时,则点P与点Q重合.
时,则点P与点Q重合.
∵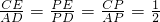
设PE=a,PC=b,则PD=2a,PA=2b,则CD2=2a×3a=b×3b,
∴ ,
,
∵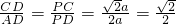 ,
,
∴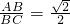 .
.
分析:(1)利用正方形的判定得出ABCD是正方形,进而得出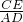 =
= ,即可得出答案;
,即可得出答案;
(2)利用已知证明出△ADQ∽△DCQ∽△ACD,进而得出QC=2AQ,以及AQ= AC=PC;
AC=PC;
(3)利用三角形面积比得出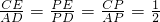 ,即可得出
,即可得出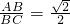 .
.
点评:此题主要考查了相似三角形的判定及性质和正方形的判定等知识,根据已知灵活应用相似三角形的性质是解决问题的关键
∴矩形ABCD是正方形,
∵AD∥EC,
∴
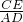 =
= ,
,∵E为BC中点,
∴
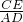 =
= =
= ,
,∴
 =
= ;
;故答案为:
 ;
;(2)∵Rt△ACD中,DQ⊥AC,
∴△ADQ∽△DCQ∽△ACD,
∴AD2=AQ•AC,CD2=CQ•AC,
∴
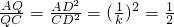

∴QC=2AQ,
又
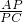 =
= =2,∴AP=2PC,
=2,∴AP=2PC,∴AQ=PQ=PC;
(3)
 .
.∵
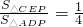 ,当
,当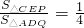 时,则点P与点Q重合.
时,则点P与点Q重合.∵
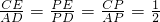
设PE=a,PC=b,则PD=2a,PA=2b,则CD2=2a×3a=b×3b,
∴
 ,
,∵
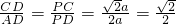 ,
,∴
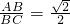 .
.分析:(1)利用正方形的判定得出ABCD是正方形,进而得出
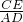 =
= ,即可得出答案;
,即可得出答案;(2)利用已知证明出△ADQ∽△DCQ∽△ACD,进而得出QC=2AQ,以及AQ=
 AC=PC;
AC=PC;(3)利用三角形面积比得出
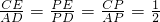 ,即可得出
,即可得出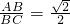 .
.点评:此题主要考查了相似三角形的判定及性质和正方形的判定等知识,根据已知灵活应用相似三角形的性质是解决问题的关键

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
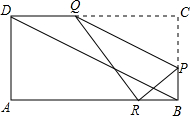
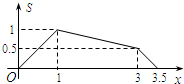
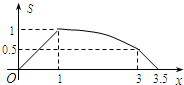
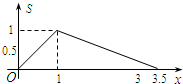
 如图所示,在矩形ABCD中,AB=1,BC=2,E是CD边的中点.点P从点A开始,沿逆时针方向在矩形边上匀速运动,到点E停止.设点P经过的路程为x,△APE的面积为S,则S关于x的函数关系的大致图象是( )
如图所示,在矩形ABCD中,AB=1,BC=2,E是CD边的中点.点P从点A开始,沿逆时针方向在矩形边上匀速运动,到点E停止.设点P经过的路程为x,△APE的面积为S,则S关于x的函数关系的大致图象是( )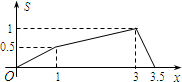
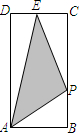
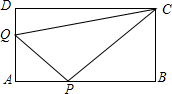 P也随之停止运动.用t表示移动时间,设四边形QAPC的面积为S.
P也随之停止运动.用t表示移动时间,设四边形QAPC的面积为S.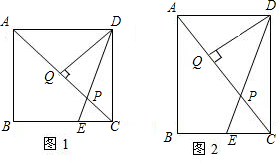 B=nBC
B=nBC 如图所示,在矩形ABCD中,AB=4cm,BC=8cm、点P从点D出发向点A运动,同时点Q从点B出发向点C运动,点P、Q的速度都是1cm/s.
如图所示,在矩形ABCD中,AB=4cm,BC=8cm、点P从点D出发向点A运动,同时点Q从点B出发向点C运动,点P、Q的速度都是1cm/s.